\(\renewcommand\AA{\unicode{x212B}}\)
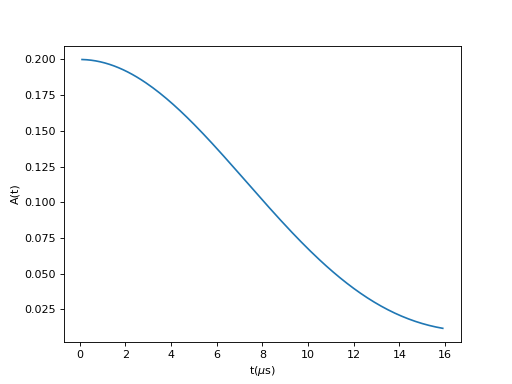
Gaussian-Broadened Gaussian Kubo-Toyabe relaxation function given by:
where \(R\) and \(\Delta^2_\text{eff}\) are defined by,
where,
\(A_0\) is the amplitude,
\(R\) the Broadening ratio,
\(\Delta_0\) is the central width,
\(\omega\) is the rms width,
and \(\Delta_{eff}\) is the effective width.
(Source code, png, hires.png, pdf)
| Name | Default | Description |
|---|---|---|
| A0 | 0.2 | |
| R | 0.1 | Broadening ratio |
| Delta0 | 0.1 | Central Field width |
[1] D.R. Noakes et al, PRB 56 2352 (1997).
[2] D.E. Maclaughlin et al, PRB 89 144419 (2014).
Categories: FitFunctions | Muon\MuonSpecific
Python: GauBroadGauKT.py (last modified: 2020-03-20)