\(\renewcommand\AA{\unicode{x212B}}\)

SpinGlass¶

Description¶

Fitting function for use by Muon scientists defined by:

\[A(t) = A_0\left(\frac{1}{3}e^{-\sqrt{\Omega t}}+\frac{2}{3}\left(1-\frac{Qa^2t^2}{\sqrt{\Omega t+Qa^2t^2}}\right)e^{-\sqrt{\Omega t + Qa^2t^2}}\right)\]

\[\Omega = \frac{4(1-Q)a^2}{\nu}\]

where,

\(A_0\) is the amplitude,

\(Q\) is the order parameter,

\(\nu\) is the rate of Markovian modulation,

and \(a\) is the half-width half maximum of the local field Lorentzian Distribution.

Note that \(0<q<1\) and \(\gamma>0\)

(Source code, png, hires.png, pdf)

Properties (fitting parameters)¶

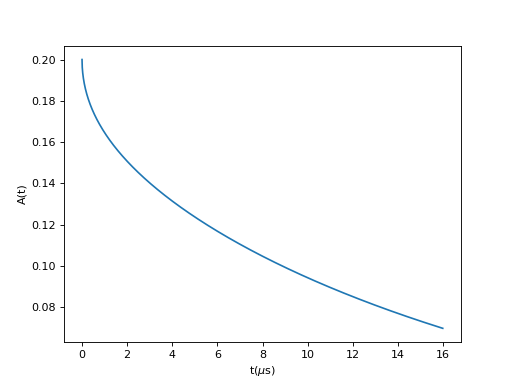
Name	Default	Description
A0	0.2	Asymmetry
Width	0.1	Half-width half maximum of the local field Lorentzian Distribution
Nu	1.0	Rate of Markovian modulation
Q	0.1	Order Parameter

References¶

[1] Y. Uemura et al., Phys. Rev. B 31 546 (1985).

Categories: FitFunctions | Muon\MuonSpecific

Source¶

Python: SpinGlass.py (last modified: 2020-03-20)