6.1

\(\renewcommand\AA{\unicode{x212B}}\)

StaticLorentzianKT

Description

Static Lorentzian Kubo-Toyabe function:

\[g_{z}^{L}(t,B_L) = A_0 \{1 - \frac{a}{\omega_{L}}j_1(\omega_{L}t)e^{-at}-\left(\frac{a}{\omega_L}\right)^2(j_o(\omega_{L}t)e^{-at}-1)-\left(1+\left(\frac{a}{\omega_L}\right)^2\right)a\int_{0}^{t}j_0(\omega_{L}\tau)e^{-a\tau}d\tau\}\]

where,

\(L\) refers to Lorentzian,

\(B_L\) refers to the longitudinal field applied to the z-axis,

\(j_{i}\) are the spheical Bessel functions of the First Kind,

\(\omega_L\) is is the precessing angular frequency and its relationship is given by \(B_L= \omega_{L} / \gamma_{\mu}\),

\(\gamma_{\mu}\) is the gyromagnetic ratio of muons,

and \(a (\mu s^{-1})\) is the half-width at half maximum of the Lorentzian distribution.

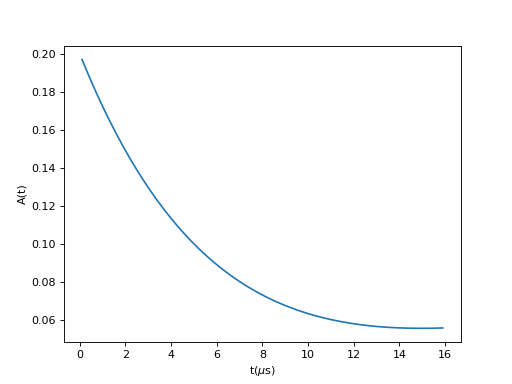
(Source code, png, hires.png, pdf)

../../_images/StaticLorentzianKT-1.png

Properties (fitting parameters)

Name Default Description
A0 0.2  
A 0.1 Half-width of half maximum of Lorentzian distribution (microsecs)
Field 0.1 Longitudinal B-field (G)

Source

Python: StaticLorentzianKT.py (last modified: 2020-03-20)