6.1

\(\renewcommand\AA{\unicode{x212B}}\)

ZFMuonium

Description

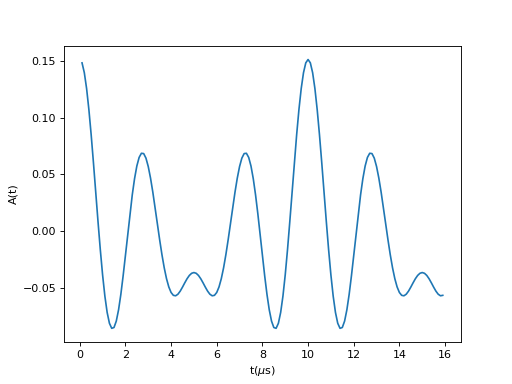
ZF rotation for axial muonium

\[A(t)=\frac{A_0}{6}\{A_1\cos(\omega_{1}+\phi)+A_2\cos(\omega_{2}+\phi)+A_{3}\cos(\omega_{3}+\phi)\}\]

and,

\[\delta= \frac{\chi}{\sqrt{1+\chi^2}},\]
\[\omega_{1}= 2\pi(\text{FreqA} - \text{FreqD}),\]
\[\omega_{2}= 2\pi\left(\text{FreqA} + \frac{\text{FreqD}}{2}\right),\]
\[\omega_{3}= 3\pi \text{FreqD},\]
\[A_{i}=\frac{1}{(1+(\omega_{i}/(2\pi F_\text{cut}))^2)}, 0<i<4\]

where,

\(A_0\) is the amplitude,

FreqA (MHz) is the isotropic hyperfine coupling constant,

FreqD (MHz) is the anisotropic hyperfine coupling constant,

\(F_\text{cut}\) is the frequency cut,

and \(\phi\) (rad) is the phase at time \(t=0\) .

(Source code, png, hires.png, pdf)

../../_images/ZFMuonium-1.png

Properties (fitting parameters)

Name Default Description
A0 0.2  
FreqA 0.3 Isotropic hyperfine coupling constant (MHz)
FreqD 0.2 Anisotropic hyperfine coupling constant (MHz)
FCut 1.0 Frequency cut (MHz)
Phi 0.0 Phase

Source

Python: ZFMuonium.py (last modified: 2020-03-20)