CalculatePlaczek v1¶

Summary¶

Calculate 1st or 2nd order Placzek correction factors using given workspace and incident spectrums.

Properties¶

Description¶

This algorithm can calculate the 1st and 2nd order Placzek inelastic scattering correction [1] [2] . For this particular algorithm:

• The input workspace must
  • contain a sample with proper chemical formula as the correction calculation relies on it.
  • have a valid instrument geometry attached to it as the correction factors are calculated on a per spectrum (i.e. detector) basis.
• A workspace containing the incident spectrum extracted from the monitor is needed.
  • For the first order correction, only the incident spectrum and its first order derivative is needed.
  • For the second order correction, the incident spectrum along with its first and second derivate are needed.
  • It is implicitly assumed that
    • IncidentSpectra.readY(0) returns the incident spectrum.
    • IncidentSpectra.readY(1) returns the first order derivative.
    • IncidentSpectra.readY(2) returns the second order derivative.
• The algorithm will try to extract temperature from the sample log if it is not provided. However, this will be a simple average without any additional consideration about outliers or bad reading. Therefore, it is recommended to provide a sample temperature in Kelvin explicitly.
• The Placzek correction calculation requires a detector efficiency curve and its derivatives. This algorithm will prioritize the use of input EfficiencySpectra. However, when EfficiencySpectra is not provided:
  • The algorithm will can generate a theoretical detector efficiency curve (see He3TubeEfficiency for details) using the input Parameter LambdaD.
  • When no LambdaD is provided, the default value 1.44 will be used, which is also the implicit value used in the original CalculatePlaczekSelfScattering.
  • Generally speaking it is better to measure the detector efficiency instead of relying on a theoretical one.
• The calculated Placzek correction factor will be scaled by the packing fraction if ScaleByPackingFraction=True (default).

where \(P\) is the Placzek correction factor, and \(p\) is the packing fraction.

Physics¶

This section provides a brief description of the formula used to calculate the Placzek correction. In the original work [1] , the formula to compute the first order Placzek correction, \(P_1\) is given as:

where

• \(\theta\) is the scattering angle.
• \(f = \frac{L_1}{L_1+L_2}\) with \(L_1\) being the distance between moderator and the sample and \(L_2\) being the distance between the sample and the detector.
• \(\phi_1\) is the first order incident flux coefficient.
• \(\epsilon_1\) is the first order detector efficiency coefficient.
• \(c_\alpha\) is the number proportion of species \(\alpha\).
• \(b_\alpha\) is the total scattering length of species \(\alpha\).
• \(m\) is the mass of neutron.
• \(M_\alpha\) refers to the atomic mass of species \(\alpha\).

When the incident flux \(\phi\) is available from monitor, the first order incident flux coefficient, \(\phi_1\) can be calculated with

where \(\phi'(\lambda)\) is defined as

When the detector efficiency \(\epsilon\) is measured as a function of wave vector \(k = 2\pi / \lambda\), the first order detector efficiency coefficient, \(\epsilon_1\) can be calculated with

However, if the detector efficiency is never measured, one can still use an approximated detector efficiency curve

where \(\lambda_d\) is the reference wavelength for the detector. Therefore, the approximate first order detector efficiency coefficient, \(\epsilon_1\) simplified to

where \(x = -\lambda / \lambda_d\). It is worth points out that the derivative of the detector efficiency is computed with respect to \(\ln(k)\), namely

The detailed explanation can be found in [2] .

(Source code, png, hires.png, pdf)

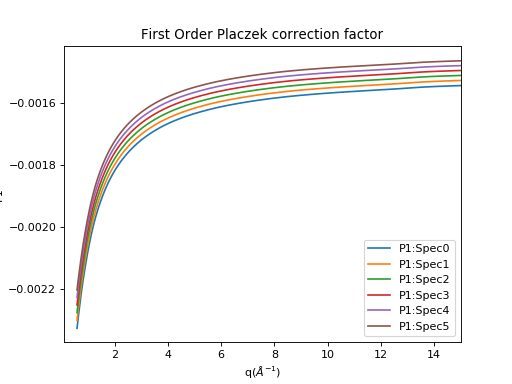
The second order Placzek correction, \(P_2\) is similar to the first order, just with some new components

where

• \(k_B\) is the Boltzmann constant.
• \(T\) is the temperature in Kelvin.
• \(E\) is the energy of the incident neutron as \(E = h^2/(2m\lambda^2_i)\).
• \(\phi_2\) is the second order incident flux coefficient.
• \(\epsilon_2\) is the second order detector efficiency coefficient.

Similar to \(\phi_1\), \(\phi_2\) can be calculated when incident flux is measured by the monitor,

and \(\epsilon_2\) can be calculated directly from measured detector efficiency,

If no detector efficiency is measured, \(\epsilon_2\) can also be approximated with the theoretical detector efficiency formula, namely

where \(x = -\lambda / \lambda_d\).

(Source code, png, hires.png, pdf)

Usage¶

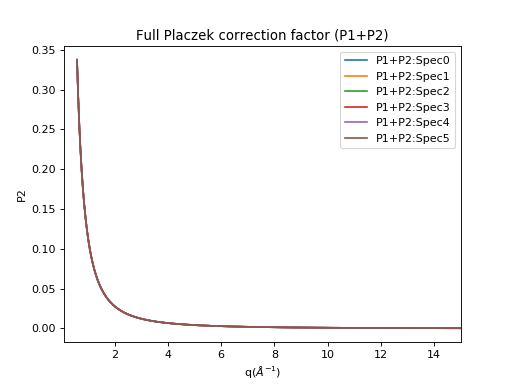
Example - CalculatePlaczek

The data files used in the following example code are available as part of the Mantid testing data.

# Load the incident flux from file
Load(
  Filename='fluxSmoothedNOM161959.nxs',
  OutputWorkspace='influx',
  )
# Load the input workspace
# - must have instrument
# - must have sample with valid chemical formula
Load(Filename='inputwsNOM_164109.nxs', OutputWorkspace='NOM_164109')

# Calculate first order
# NOTE: temperature is not needed for first order calculation
CalculatePlaczek(
 InputWorkspace="NOM_164109",
 IncidentSpectra="influx",
 LambdaD=1.44,
 Order=1,
 ScaleByPackingFraction=False,
 CrystalDensity=0.01,
 OutputWorkspace="NOM_P1",
 )

# Calculate first and second order
CalculatePlaczek(
 InputWorkspace="NOM_164109",
 IncidentSpectra="influx",
 LambdaD=1.44,
 Order=2,
 SampleTemperature=943.15,  # in Kelvin
 ScaleByPackingFraction=False,
 CrystalDensity=0.01,
 OutputWorkspace="NOM_P2",
)

References¶

Categories: AlgorithmIndex | CorrectionFunctions

Source¶

C++ header: CalculatePlaczek.h (last modified: 2021-08-27)

C++ source: CalculatePlaczek.cpp (last modified: 2021-08-30)