\(\renewcommand\AA{\unicode{x212B}}\)
Table of Contents
Adds fake multi-dimensional event data to an existing MDEventWorkspace, for use in testing. You can create a blank MDEventWorkspace with CreateMDWorkspace.
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | InOut | MDEventWorkspace | Mandatory | An input workspace, that will get DataObjects added to it |
| UniformParams | Input | dbl list | Add a uniform, randomized distribution of events. 1 parameter: number_of_events; they will be distributed across the size of the workspace. Depending on the sign of this parameter, the events are either distributed randomly around the box (Case 1, positive) or placed on the regular grid through the box (Case 2, negative) Treatment of Multiple parameters: depends on the Case Case 1: number_of_events, min,max (for each dimension); distribute the events inside the range given. Case 2: Additional parameters describe initial location and steps of the regular grid in each dimension | |
| PeakParams | Input | dbl list | Add a peak with a normal distribution around a central point. Parameters: number_of_events, x, y, z, …, radius. | |
| EllipsoidParams | Input | dbl list | Add an nd ellipsoidal peak with a multivariate normal distribution around a central point (x1,…x_N). The ellipsoid is defined by an N eigenvectors with N elements and N eigenvalues which correpsond to the variance along the principal axes. The final argument is doCounts which can be either negative or positive. If doCounts<0 then all events have a count of 1, else if doCounts>0 then the counts of each event is determined by the Mahalanobis distance https://en.wikipedia.org/wiki/Mahalanobis_distance Parameters: number_of_events, x_1,..,x_N, eigvect_1(1),…,eigvect_1(N), …, eigvect_N(1),..eigvect_N(N), eigval_1,…,eigval_N, doCounts. | |
| RandomSeed | Input | number | 0 | Seed int for the random number generator. |
| RandomizeSignal | Input | boolean | False | If true, the events’ signal and error values will be randomized around 1.0+-0.5. |
For testing MDEventWorkspaces, this algorithm either creates a uniform, random distribution of events, or generates regular events placed in boxes, or fills peaks around given points with a given number of events.
This algorithm can be run on a pre-existing MDEventWorkspace or a newly created one. All of the examples below will be done with newly created ones using CreateMDWorkspace.
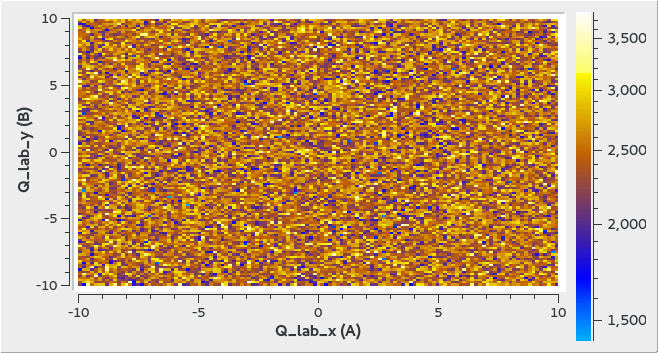
2D Uniform Event Distribution Example
ws = CreateMDWorkspace(Dimensions='2', EventType='MDEvent', Extents='-10,10,-10,10',
Names='Q_lab_x,Q_lab_y', Units='A,B')
FakeMDEventData(ws, UniformParams="1000000")
print("Number of events = {}".format(ws.getNEvents()))
Output:
Number of events = 1000000
The output looks like the following in the Sliceviewer:
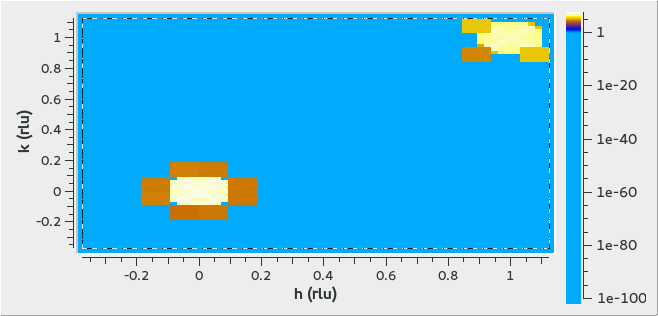
3D Peaks Example
Creates 3 peaks in (H,K,L) at (0,0,0), (1,1,0) and (1,1,1).
ws = CreateMDWorkspace(Dimensions='3', Extents='-3,3,-3,3,-3,3', Names='h,k,l',
Units='rlu,rlu,rlu', SplitInto='4')
FakeMDEventData(ws, PeakParams='10000,1,1,1,0.1', RandomSeed='63759', RandomizeSignal='1')
FakeMDEventData(ws, PeakParams='100000,0,0,0,0.1', RandomSeed='63759', RandomizeSignal='1')
FakeMDEventData(ws, PeakParams='40000,1,1,0,0.1', RandomSeed='63759', RandomizeSignal='1')
print("Number of events = {}".format(ws.getNEvents()))
Output:
Number of events = 150000
The output looks like the following in the Sliceviewer:
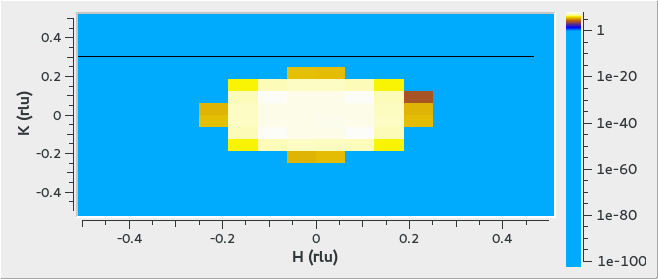
4D Peaks Example
Creates a peak at (H,K,L) of (0,0,0) around T=5K.
ws = CreateMDWorkspace(Dimensions='4', Extents='-1,1,-1,1,-1,1,0,10', Names='H,K,L,T', Units='rlu,rlu,rlu,K',
SplitInto='2', SplitThreshold='50')
FakeMDEventData(ws, PeakParams='1e+06,0,0,0,5,0.2', RandomSeed='3873875')
print("Number of events = {}".format(ws.getNEvents()))
Output:
Number of events = 1000000
The output looks like the following in the Sliceviewer when the T slider is moved to ~5K:
Categories: AlgorithmIndex | MDAlgorithms\Creation