\(\renewcommand\AA{\unicode{x212B}}\)
A Gaussian function (also referred to as a normal distribution) is defined as:
where
Note that the FWHM (Full Width Half Maximum) of a Gaussian equals \(2\sqrt{2\ln 2}*\mbox{Sigma}\).
The integrated peak intensity for the Gaussian is given by \(\mbox{height} * \mbox{sigma} * \sqrt{2\pi}\).
The uncertainty for the intensity is: \(\mbox{intensity} * \sqrt{\left(\frac{\delta \mbox{height}}{\mbox{height}}\right)^2 + \left(\frac{\delta \mbox{sigma}}{\mbox{sigma}}\right)^2}\).
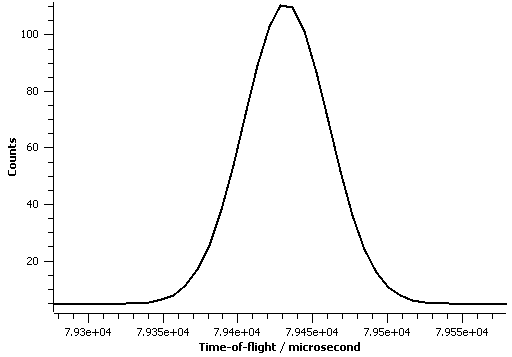
The figure below illustrate this symmetric peakshape function fitted to a TOF peak:
| Name | Default | Description |
|---|---|---|
| Height | 0.0 | Height of peak |
| PeakCentre | 0.0 | Centre of peak |
| Sigma | 0.0 | Width parameter |
Categories: FitFunctions | Peak | Muon\MuonModelling