6.4

\(\renewcommand\AA{\unicode{x212B}}\)

NeutronBk2BkExpConvPVoigt

Description

Notice

1. This is not an algorithm. However this fit function is a used through the Fit v1 algorithm.

  1. It is renamed from ThermalNeutronBk2BkExpConvPV.

3. ThermalNeutronBk2BkExpConvPVoigt is not a regular peak function to fit individual peaks. It is not allowed to set FWHM or peak centre to this peak function.

Summary

A thermal neutron back-to-back exponential convoluted with pseuduo-voigt peakshape function is indeed a back-to-back exponential convoluted with pseuduo-voigt peakshape function, while the parameters \(\alpha, \beta, \sigma\) are not directly given, but calculated from a set of parameters that are universal to all peaks in powder diffraction data.

The purpose to implement this peak shape is to perform Le Bail Fit and other data analysis on time-of-flight powder diffractometers’ data in Mantid. It is the peak shape No. 10 in Fullprof. See Refs. 1.

Description

Thermal neutron back to back exponential convoluted with pseudo voigt peak function is a back to back exponential convoluted with pseudo voigt peak function. Its difference to a regular back to back exponential convoluted with pseudo voigt peak functiont is that it is a function for all peaks in a TOF powder diffraction pattern, but not a single peak.

Furthermore, the purpose to implement this function in Mantid is to refine multiple parameters including crystal sample’s unit cell parameters. Therefore, unit cell lattice parameters are also included in this function.

Methods are not supported

1. setFWHM() 2. setCentre() : peak centre is determined by a set of parameters including lattice parameter, Dtt1, Dtt1t, Zero, Zerot, Dtt2t, Width and Tcross. Therefore, it is not allowed to set peak centre to this peak function.

Back-to-back exponential convoluted with pseuduo-voigt peakshape function

A back-to-back exponential convoluted with pseuduo-voigt peakshape function for is defined as

\[\Omega(X_0) = \int_{\infty}^{\infty}pV(X_0-t)E(t)dt\]

For back-to-back exponential:

\[E(d, t) = 2Ne^{\alpha(d) t} (t \leq 0)\]
\[E(d, t) = 2Ne^{-\beta(d) t} (t \geq 0)\]
\[N(d) = \frac{\alpha(d)\beta(d)}{2(\alpha(d)+\beta(d))}\]

For psuedo-voigt

\[pV(x) = \eta L'(x) + (1-\eta)G'(x)\]

The parameters \(/alpha\) and \(/beta\) represent the absolute value of the exponential rise and decay constants (modelling the neutron pulse coming from the moderator) , L’(x) stands for Lorentzian part and G’(x) stands for Gaussian part. The parameter \(X_0\) is the location of the peak; more specifically it represent the point where the exponentially modelled neutron pulse goes from being exponentially rising to exponentially decaying.

References

  1. Fullprof manual

The figure below illustrate this peakshape function fitted to a TOF peak:

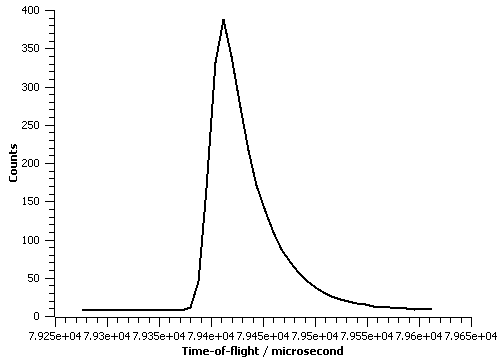
BackToBackExponentialWithConstBackground.png

Formula for converting unit from d-spacing to TOF

Parameters of back-to-back exponential convoluted psuedo-voigt function are calculated from a set of parameters universal to all peaks in a diffraction pattern. Therefore, they are functions of peak position, \(d\).

\[ \begin{align}\begin{aligned}n_{cross} = \frac{1}{2} erfc(Width(xcross\cdot d^{-1}))\\TOF_e = Zero + Dtt1\cdot d\\TOF_t = Zerot + Dtt1t\cdot d - Dtt2t \cdot d^{-1}\end{aligned}\end{align} \]

Final Time-of-flight is calculated as:

\[TOF = n_{cross} TOF_e + (1-n_{cross}) TOF_t`\]

Formula for calculating \(A(d)\), \(B(d)\), \(\sigma(d)\) and \(\gamma(d)\)

\(\alpha(d)\):

\[ \begin{align}\begin{aligned}\alpha^e(d) = \alpha_0^e + \alpha_1^e d_h\\\alpha^t(d) = \alpha_0^t - \frac{\alpha_1^t}{d_h}\\\alpha(d) = \frac{1}{n\alpha^e + (1-n)\alpha^t}\end{aligned}\end{align} \]

\(\beta(d)\):

\[ \begin{align}\begin{aligned}\beta^e(d) = \beta_0^e + \beta_1^e d_h\\\beta^t(d) = \beta_0^t - \frac{\beta_1^t}{d_h}\\\beta(d) = \frac{1}{n\alpha^e + (1-n)\beta^t}\end{aligned}\end{align} \]

For \(\sigma_G\) and \(\gamma_L\), which represent the standard deviation for pseudo-voigt

\[ \begin{align}\begin{aligned}\begin{split}\sigma_G^2(d_h) = \sigma_0^2 + (\sigma_1^2 + DST2(1-\zeta)^2)d_h^2 + (\sigma_2^2 + Gsize)d_h^4 \\\end{split}\\\gamma_L(d_h) = \gamma_0 + (\gamma_1 + \zeta\sqrt{8\ln2DST2})d_h + (\gamma_2+F(SZ))d_h^2\end{aligned}\end{align} \]

The analysis formula for the convoluted peak at \(d_h\)

\[\Omega(TOF(d_h)) = (1-\eta(d_h))N\{e^uerfc(y)+e^verfc(z)\} - \frac{2N\eta}{\pi}\{\Im[e^pE_1(p)]+\Im[e^qE_1(q)]\}\]

where

\[ \begin{align}\begin{aligned}erfc(x) = 1-erf(x) = 1-\frac{2}{\sqrt{\pi}}\int_0^xe^{-u^2}du\\E_1(z) = \int_z^{\infty}\frac{e^{-t}}{t}dt\\u = \frac{1}{2}\alpha(d_h)(\alpha(d_h)\sigma^2(d_h)+2x)\\y = \frac{\alpha(d_h)\sigma^2(d_h)+x}{\sqrt{2\sigma^2(d_h)}}\\p = \alpha(d_h)x + \frac{i\alpha(d_h)H(d_h)}{2}\\v = \frac{1}{2}\beta(d_h)(\beta(d_h)\sigma^2(d_h)-2x)\\z = \frac{\beta(d_h)\sigma^2(d_h)-x}{\sqrt{2\sigma^2(d_h)}}\\q = -\beta(d_h)x + \frac{i\beta(d_h)H(d_h)}{2}\end{aligned}\end{align} \]

\(erfc(x)\) and \(E_1(z)\) will be calculated numerically.

Properties (fitting parameters)

Name Default Description
Height 1.0 Intensity of peak
Dtt1 1.0 coefficient 1 for d-spacing calculation for epithermal neutron part
Dtt2 1.0 coefficient 2 for d-spacing calculation for epithermal neutron part
Zero 0.0 Zero shift for epithermal neutron
Alph0 1.6 exponential constant for rising part of epithermal neutron pulse
Alph1 1.5 exponential constant for rising part of expithermal neutron pulse
Beta0 1.6 exponential constant of decaying part of epithermal neutron pulse
Beta1 1.5 exponential constant of decaying part of epithermal neutron pulse
Sig0 1.0 variance parameter 1 of the Gaussian component of the psuedovoigt function
Sig1 1.0 variance parameter 2 of the Gaussian component of the psuedovoigt function
Sig2 1.0 variance parameter 3 of the Gaussian component of the psuedovoigt function
Gam0 0.0 FWHM parameter 1 of the Lorentzian component of the psuedovoigt function
Gam1 0.0 FWHM parameter 2 of the Lorentzian component of the psuedovoigt function
Gam2 0.0 FWHM parameter 3 of the Lorentzian component of the psuedovoigt function
LatticeConstant 10.0 lattice constant for the sample
H 0.0 Miller index H.
K 0.0 Miller index K.
L 0.0 Miller index L.

Categories: FitFunctions | General