\(\renewcommand\AA{\unicode{x212B}}\)

ComputeIncoherentDOS v1

../_images/ComputeIncoherentDOS-v1_dlg.png

ComputeIncoherentDOS dialog.

Summary

Calculates the neutron weighted generalised phonon density of states in the incoherent approximation from a measured powder INS MatrixWorkspace

Properties

Name

Direction

Type

Default

Description

InputWorkspace

Input

MatrixWorkspace

Mandatory

Input MatrixWorkspace containing the reduced inelastic neutron spectrum in (Q,E) or (2theta,E) space.

Temperature

Input

number

300

Sample temperature in Kelvin.

MeanSquareDisplacement

Input

number

0

Average mean square displacement in Angstrom^2.

QSumRange

Input

string

0,Qmax

Range in Q (in Angstroms^-1) to sum data over.

EnergyBinning

Input

string

0,Emax/50,Emax*0.9

Energy binning parameters [Emin, Emax] or [Emin, Estep, Emax] in meV.

Wavenumbers

Input

boolean

False

Should the output be in Wavenumbers (cm^-1)?

StatesPerEnergy

Input

boolean

False

Should the output be in states per unit energy rather than mb/sr/fu/energy? (Only for pure elements, need to set the sample material information)

OutputWorkspace

Output

MatrixWorkspace

Mandatory

Output workspace name.

TwoThetaSumRange

Input

string

Twothetamin, Twothetamax

Range in 2theta (in degrees) to sum data over.

Description

Computes the phonon density of states from an inelastic neutron scattering measurement of a powder or polycrystalline sample, assuming that all scattering is incoherent, using the formula for the 1-phonon incoherent scattering function [1]:

\[S^{(1)}_{\mathrm{inc}}(Q,E) = \exp\left(-2\bar{W}(Q)\right) \frac{Q^2}{E} \left< n+\frac{1}{2}\pm\frac{1}{2} \right> \left[ \sum_k \frac{\sigma_k^{\mathrm{scatt}}}{2m_k} g_k(E) \right],\]

where the term in square brackets is the neutron weighted density of states which is calculated by this algorithm, and \(g_k(E)\) is the partial density of states for each component (element or isotope) \(k\) in the material. \(m_k\) is the relative atomic mass of the component.

The average Debye-Waller factor \(\exp\left(-2\bar{W}(Q)\right)\) is calculated using an average mean-square displacement \(\langle u^2 \rangle\), using \(W=Q^2\langle u^2\rangle/2\).

The algorithm accepts both \(S(Q,E)\) workspaces as well as \(S(2\theta,E)\) workspaces. In the latter case \(Q\) values are calculated from \(2\theta\) and \(E\) before applying the formula above. Note, that QSumRange is only applicable with \(S(Q,E)\) while TwoThetaSumRange works only for \(S(2\theta,E)\).

If the data has been normalised to a Vanadium standard measurement, the output of this algorithm is the neutron weighted density of states in milibarns/steradians per formula unit per meV (or per cm^-1). If the sample material has been set and is found to be a pure element, then an additional option will be enabled to calculate the DOS in states per meV (states per cm^-1) by dividing by the scattering cross-section and multiplying by the relative atomic mass.

Restrictions on the Input Workspace

The input workspace must have units of Momentum Transfer or Degrees and contain histogram data with common binning on all spectra.

Usage

Note

To run these usage examples please first download the usage data, and add these to your path. In Mantid this is done using Manage User Directories.

ISIS Example

The following code will run a reduction on a MARI (ISIS) dataset and apply the algorithm to the reduced data. The datafiles (runs 21334, 21335, 21347) and map file ‘mari_res2013.map’ should be in your path. Run number 21335 is a measurement of a large Aluminium sample from the neutron training course.

from Direct import DirectEnergyConversion
from mantid.simpleapi import *
rd = DirectEnergyConversion.DirectEnergyConversion('MARI')
ws = rd.convert_to_energy(21334, 21335, 60, [-55,0.05,55], 'mari_res2013.map',
    monovan_run=21347, sample_mass=106.4, sample_rmm=27, monovan_mapfile='mari_res2013.map')
ws_sqw = SofQW3(ws, [0,0.1,12], 'Direct', 60)
SetSampleMaterial(ws_sqw,'Al')
ws_dos = ComputeIncoherentDOS(ws_sqw, Temperature=5, StatesPerEnergy=True)

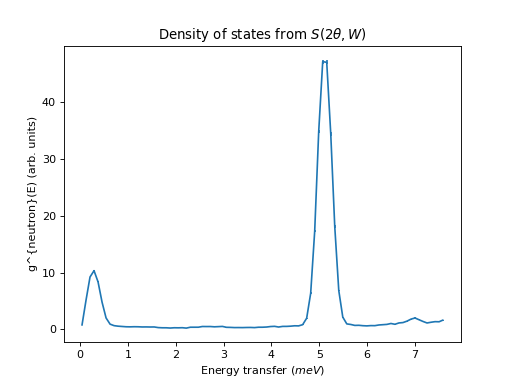
ILL Example using S(2theta, E) as input

from mantid import mtd
from mantid.simpleapi import *
import matplotlib.pyplot as plt

ws = DirectILLCollectData('ILL/IN4/087294.nxs')
DirectILLReduction(ws, OutputWorkspace='sqw', OutputSofThetaEnergyWorkspace='stw')
temperature = ws.run().getProperty('sample.temperature').value
dos = ComputeIncoherentDOS('stw',  Temperature=temperature, EnergyBinning='0, Emax')

fig, axis = plt.subplots(subplot_kw={'projection':'mantid'})
axis.errorbar(dos)
axis.set_title('Density of states from $S(2\\theta,W)$')
# Uncomment the line below to show the plot.
#fig.show()
mtd.clear()

(Source code, png, hires.png, pdf)

../_images/ComputeIncoherentDOS-v1-1.png

Test Example

This example uses a generated dataset so that it will run on automated tests of the build system where the above datafiles do not exist.

ws = CreateSampleWorkspace(binWidth = 0.1, XMin = 0, XMax = 50, XUnit = 'DeltaE')
ws = ScaleX(ws, -25, "Add")
LoadInstrument(ws, InstrumentName='MARI', RewriteSpectraMap = True)
ws = SofQW(ws, [0, 0.05, 8], 'Direct', 25)
ws_DOS = ComputeIncoherentDOS(ws)

References

Categories: AlgorithmIndex | Inelastic

Source

Python: ComputeIncoherentDOS.py