\(\renewcommand\AA{\unicode{x212B}}\)

PDConvertReciprocalSpace v1

PDConvertReciprocalSpace dialog.

Summary

Transforms a Workspace2D between different reciprocal space functions.

See Also

PDConvertRealSpace

Properties

Name	Direction	Type	Default	Description
InputWorkspace	Input	MatrixWorkspace	Mandatory	Input workspace with units of momentum transfer
From	Input	string	S(Q)	Function type in the input workspace. Allowed values: [‘S(Q)’, ‘F(Q)’, ‘FK(Q)’, ‘DCS(Q)’]
To	Input	string	S(Q)	Function type in the output workspace. Allowed values: [‘S(Q)’, ‘F(Q)’, ‘FK(Q)’, ‘DCS(Q)’]
OutputWorkspace	Output	Workspace	Mandatory	Output workspace

Description

The neutron diffraction is measuring the differential scattering cross section (DCS(Q) in the algorithm)

(1)\[\frac{d\sigma}{d\Omega} = \frac{N}{\phi d\Omega}\]

Here the \(N\) is the number of scattered neutrons in unit time in a solid angle \(d\Omega\), and \(\phi\) is the incident neutron flux. The algorithm supports the following conversions:

(2)\[S(Q) = \frac{1}{N_{s} \langle b_{coh} \rangle^2}\frac{d\sigma}{d\Omega}(Q) - \frac{\langle b_{tot}^2 \rangle - \langle b_{coh} \rangle^2}{\langle b_{coh} \rangle^2}\]

(3)\[F(Q) = Q [S(Q) - 1]\]

(4)\[F_K(Q) = \langle b_{coh} \rangle^2 [S(Q) - 1] = \frac{\langle b_{coh} \rangle^2}{Q} F(Q)\]

where \(N_s\) is the number of scatters in the sample and both \(\langle b_{tot}^2 \rangle\) and \(\langle b_{coh} \rangle^2\) are defined in the Materials concept page.

NOTE: This algorithm requires that SetSampleMaterial v1 is called prior in order to determine the \(\langle b_{tot}^2 \rangle\) and \(\langle b_{coh} \rangle^2\) terms.

PyStoG

This algorithm uses the external project PyStoG and specifically uses the pystog.converter.Converter object. To modify the underlying algorithms, the following functions are used for the conversions.

• \(\frac{d\sigma}{d\Omega}(Q)\) conversions are:

  • To \(F(Q)\) see pystog.converter.Converter.DCS_to_F()

  • To \(F_K(Q)\) see pystog.converter.Converter.DCS_to_FK()

  • To \(S(Q)\) see pystog.converter.Converter.DCS_to_S()

• \(S(Q)\) conversions are:

  • To \(F(Q)\) see pystog.converter.Converter.S_to_F()

  • To \(F_K(Q)\) see pystog.converter.Converter.S_to_FK()

  • To \(\frac{d\sigma}{d\Omega}(Q)\) see pystog.converter.Converter.S_to_DCS()

• \(F(Q)\) conversions are:

  • To \(\frac{d\sigma}{d\Omega}(Q)\) see pystog.converter.Converter.F_to_DCS()

  • To \(F_K(Q)\) see pystog.converter.Converter.F_to_FK()

  • To \(S(Q)\) see pystog.converter.Converter.F_to_S()

• \(F_K(Q)\) conversions are:

  • To \(\frac{d\sigma}{d\Omega}(Q)\) see pystog.converter.Converter.FK_to_DCS()

  • To \(F(Q)\) see pystog.converter.Converter.FK_to_F()

  • To \(S(Q)\) see pystog.converter.Converter.FK_to_S()

Usage

import wget
import numpy as np
import matplotlib.pyplot as plt
from mantid.simpleapi import CreateWorkspace, SetSampleMaterial, PDConvertReciprocalSpace
from mantid import plots

# Grab the reciprocal data for argon
url = "https://raw.githubusercontent.com/marshallmcdonnell/pystog/master/tests/test_data/argon.reciprocal_space.dat"
filename = wget.download(url)
q, sq, fq_, fk_, dcs_ = np.loadtxt(filename, skiprows=2, unpack=True)

# Convert S(Q) to Mantid wksp
s_of_q = CreateWorkspace(DataX=q, DataY=sq,
                       UnitX="MomentumTransfer",
                       Distribution=True)
SetSampleMaterial(InputWorkspace=s_of_q, ChemicalFormula='Ar')
f_of_q=PDConvertReciprocalSpace(InputWorkspace=s_of_q, From='S(Q)', To='F(Q)')
fk_of_q=PDConvertReciprocalSpace(InputWorkspace=s_of_q, From='S(Q)', To='FK(Q)')
dcs_of_q=PDConvertReciprocalSpace(InputWorkspace=s_of_q, From='S(Q)', To='DCS(Q)')

fig, ax = plt.subplots(subplot_kw={'projection':'mantid'})
ax.plot(s_of_q,'k-', label='$S(Q)$')
ax.plot(f_of_q,'r-', label='$F(Q)$')
ax.plot(fk_of_q,'b-', label='$F_K(Q)$')
ax.plot(dcs_of_q,'g-', label='$d\sigma / d\Omega(Q)$')
ax.legend() # show the legend
fig.show()

The output should look like:

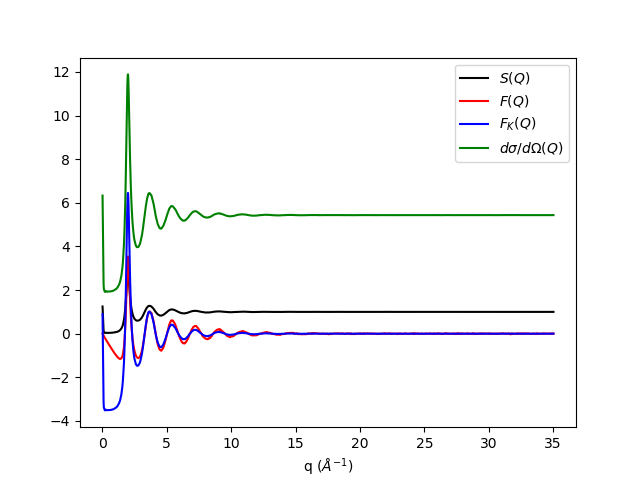
Categories: AlgorithmIndex | Diffraction\Utility

Source

Python: PDConvertReciprocalSpace.py