\(\renewcommand\AA{\unicode{x212B}}\)
BackToBackExponential¶
Description¶
A back-to-back exponential peakshape function is defined as:
This peakshape function represent the convolution of back-to-back exponentials and a Gaussian function and is designed to be used for the data analysis of time-of-flight (TOF) neutron powder diffraction data, see Ref. 1.
The parameters \(A\) and \(B\) represent the absolute value of the exponential rise and decay constants (modelling the neutron pulse coming from the moderator) and \(S\) represent the standard deviation of the Gaussian. The parameter \(X0\) is the location of the peak; more specifically it represent the point where the exponentially modelled neutron pulse goes from being exponentially rising to exponentially decaying. In general \(X0\) does not conicide with the maximum of the peak (it is typically at slightly lower TOF than the maximum, by an amount that depends on \(A\), \(B\) and \(S\)). \(I\) is the integrated intensity.
For information about how to convert Fullprof back-to-back exponential parameters into those used for this function see CreateBackToBackParameters. For information about how to create parameters from a GSAS parameter file see CreateBackToBackParametersGSAS.
References
1. R.B. Von Dreele, J.D. Jorgensen & C.G. Windsor, J. Appl. Cryst., 15, 581-589, 1982
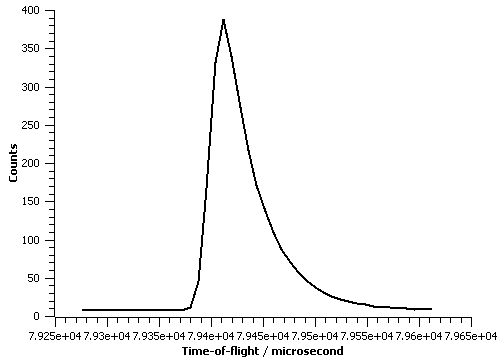
The figure below illustrate this peakshape function fitted to a TOF peak:
Properties (fitting parameters)¶
Name |
Default |
Description |
|---|---|---|
I |
0.0 |
integrated intensity of the peak |
A |
1.0 |
exponential constant of rising part of neutron pulse |
B |
0.05 |
exponential constant of decaying part of neutron pulse |
X0 |
0.0 |
peak position |
S |
1.0 |
standard deviation of gaussian part of peakshape function |
Note
the initial default guesses for in particular A and B are only based on fitting a couple of peaks in a dataset collected on the ISIS’s HRPD instrument.
Categories: FitFunctions | Peak
Source¶
C++ header: BackToBackExponential.h
C++ source: BackToBackExponential.cpp
