\(\renewcommand\AA{\unicode{x212B}}\)
Lorentzian¶
Description¶
A Lorentzian function is defined as:
\[\frac{A}{\pi} \left( \frac{\frac{\Gamma}{2}}{(x-x_0)^2 + (\frac{\Gamma}{2})^2}\right)\]
where:
A (Amplitude) - Intensity scaling
\(x_0\) (PeakCentre) - centre of peak
\(\Gamma/2\) (HWHM) - half-width at half-maximum
Note that the FWHM (Full Width Half Maximum) equals two times HWHM, and the integral over the Lorentzian equals the intensity scaling A.
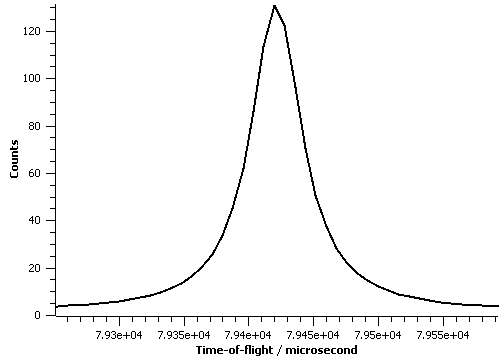
The figure below illustrate this symmetric peakshape function fitted to a TOF peak:
Properties (fitting parameters)¶
Name |
Default |
Description |
|---|---|---|
Amplitude |
1.0 |
Intensity scaling |
PeakCentre |
0.0 |
Centre of peak |
FWHM |
0.0 |
Full-width at half-maximum |
Categories: FitFunctions | Peak | Muon\MuonModelling
Source¶
C++ header: Lorentzian.h
C++ source: Lorentzian.cpp
