\(\renewcommand\AA{\unicode{x212B}}\)

FindSatellitePeaks v1

Enable screenshots using DOCS_SCREENSHOTS in CMake

Summary

Algorithm for finding satellite peaks in an MDWorkspace in the HKL frame.

Properties

Name	Direction	Type	Default	Description
NuclearPeaks	Input	PeaksWorkspace	Mandatory	Main integer HKL peaks. Q vectors will be calculated relative to these peaks.
SatellitePeaks	Input	PeaksWorkspace	Mandatory	Positions of seed satellite peaks. These will be used to define the modulation (q) vectors for each satellite.
MDWorkspace	Input	Workspace	Mandatory	MD workspace to search for satellites peak in. This data must be in the HKL frame.
OutputWorkspace	Output	PeaksWorkspace	Mandatory	All found satellite peaks. These will be given with satellite coordinates.
NumOfQs	Input	long	-1	The number of satellite peaks to look for. If this option is not set to the default then all the provided satellites will be grouped into exactly this number of modulation (q) vectors
ClusterThreshold	Input	number	1.5	Threshold for automaticallty deciding on the number of modulation (q) vectors to use. If NumOfQs found is set then this is property is ignored.
PeakRadius	Input	number	0.1	The peak radius used to integrate the satellite peaks. This is Euclidean distance in HKL space. This is passed directly to IntegratePeaksMD
BackgroundInnerRadius	Input	number	0.1	The inner background radius used to integrate the satellite peaks. This is Euclidean distance in HKL space. This is passed directly to IntegratePeaksMD
BackgroundOuterRadius	Input	number	0.2	The outer background radius used to integrate satellite peaks. This is Euclidean distance in HKL space. his is passed directly to IntegratePeaksMD
IOverSigma	Input	long	2	The I/sigma threshold use to identify if peaks exist. This is passed direclty to FilterPeaks

Description

FindSatellitePeaks can be used to refine the locations of “satellite” peaks occurring at fractional HKL locations in reciprocal space. FindSatellitePeaks takes a MDWorkspace of experimental data, a PeaksWorkspace containing the locations of peaks with integer HKL, and another PeaksWorkspace containing a subset of peaks found at fractional HKL.

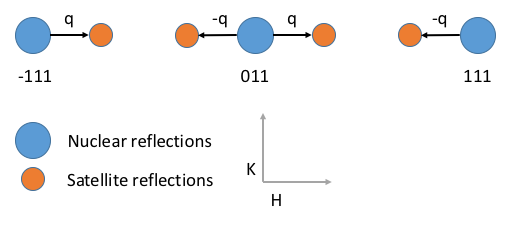
Satellite peaks exist at fractional HKL coordinates. The vector q is the Euclidean distance from the nearest integer HKL peak to the satellite. A schematic of this is shown in the HKL plane in the diagram above.

For each satellite peak the euclidean distance between the nearest integer peak and satellite are computed in the HKL frame. Peaks are then grouped according to euclidean distance using using the properties NumOfQs and ClusterThreshold. If NumOfQs is specified then each offset will be grouped into exactly k clusters. If ClusterThreshold is specified then offsets will be grouped into clusters separated by no more than a cophenetic distance below this threshold. The centroid of each cluster calculated for each group and is used as the offset to predict the location of fractional peaks everywhere in the MDWorkspace.

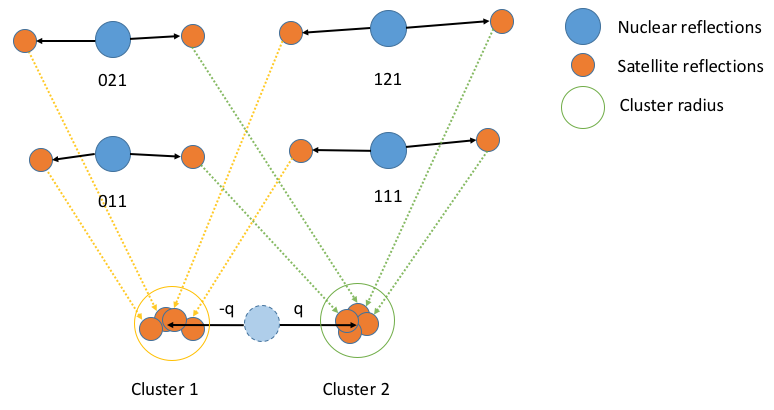
Due to noise in the experimental data the q vector for every satellite may vary slightly. This algorithm calculates the q vectors for all peaks passed as starting points into distinct sets of q vectors. The centroid of each cluster is then taken as the “true” value of q and is used to predict the position of all other fractional peaks with this q.

For each predicted fractional peak, the local centroid (the radius of which is defined by PeakRadius) in the MD data is found and this is taken as the actual position of the satellite peaks.

Finally the found satellite peaks are integerated using the IntegratePeaksMD algorithm with the parameters PeakRadius, BackgroundInnerRadius, and BackgroundOuterRadius. Satellite peaks are discarded if there I/sigma value is less than the parameter IOverSigma.

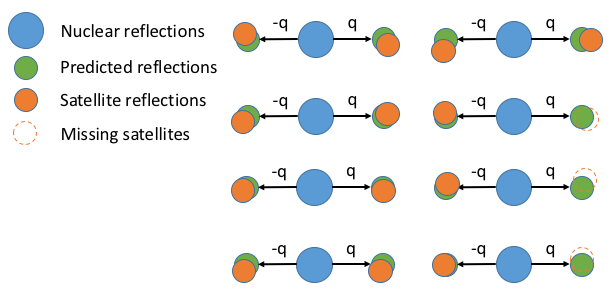
Finally, using the predicted satellite peak positions (green) the local centroid is found and this is used as the true position of the experimental satellite peak (orange). The area to search for the centroid is controlled by the PeakRadius parameter. All centroids are integrated a filtered by intensity and \(\frac{I}{\sigma}\). If the experimental satellite has zero intensity or is below the \(\frac{I}{\sigma}\) threshold then it is discarded.

The output of the algorithm is a peaks workspace containing all of the satellite peaks found by the algorithm in fractional coordinates. Each of the peaks will have an intensity value from the IntegratePeaksMD algorithm.

Warning

This integration is very approximate and may not produce the best possible values. It is recommended that satellite peaks are reintegrated using one of the many peak integration algorithms and to tune their parameters to obtain the best possible peak integration.

For more information on superspace crystallography see:

• Van Smaalen, Sander. “An elementary introduction to superspace crystallography.” Zeitschrift für Kristallographie-Crystalline Materials 219, no. 11 (2004): 681-691.

• Van Smaalen, Sander. “Incommensurate crystal structures.” Crystallography Reviews 4, no. 2 (1995): 79-202.

Related Algorithms

• PredictFractionalPeaks predicts the position of fractional peaks given a PeaksWorkspace of nuclear peaks and a set of HKL offsets.

• CentroidPeaksMD is used to find the local centroid from a predicted peak position.

• IntegratePeaksMD is used to integrate satellite peaks to check if they actually exist at the predicted position.

• FilterPeaks is used to remove peaks with zero intensity or a I/sigma below the desired threshold.

• IndexSatellitePeaks can be used to obtain a superspace indexing of the peaks workspace output from this algorithm.

Usage

Note

To run these usage examples please first download the usage data, and add these to your path. In Mantid this is done using Manage User Directories.

Example - calling FindSatellitePeaks:

md_workspace = Load(Filename='WISH_md_small.nxs', OutputWorkspace='WISH_md_small')
satellite_peaks = Load(Filename='WISH_peak_hkl_frac_small.nxs', OutputWorkspace='WISH_peak_hkl_frac_small')
main_peaks = Load(Filename='WISH_peak_hkl_small.nxs',OutputWorkspace='WISH_peak_hkl_small')

params = {
    "PeakRadius": 0.3,
    "BackgroundInnerRadius": 0.3,
    "BackgroundOuterRadius": 0.4,
    "OutputWorkspace": "refined_peaks",
    "NumOfQs": 2
}


satellites_refined = FindSatellitePeaks(NuclearPeaks=main_peaks, SatellitePeaks=satellite_peaks, MDWorkspace=md_workspace, **params)

print (len(satellites_refined))

Output:

4

Categories: AlgorithmIndex | Crystal\Peaks

Source

Python: FindSatellitePeaks.py