\(\renewcommand\AA{\unicode{x212B}}\)

PDConvertRealSpace v1

Enable screenshots using DOCS_SCREENSHOTS in CMake

Summary

Transforms a Workspace2D between different real space functions.

See Also

PDConvertReciprocalSpace

Properties

Name	Direction	Type	Default	Description
InputWorkspace	Input	MatrixWorkspace	Mandatory	Input workspace. The units are assumed to be distance
From	Input	string	G(r)	Function type in the input workspace. Allowed values: [‘G(r)’, ‘GK(r)’, ‘g(r)’]
To	Input	string	G(r)	Function type in the output workspace. Allowed values: [‘G(r)’, ‘GK(r)’, ‘g(r)’]
OutputWorkspace	Output	Workspace	Mandatory	Output workspace

Description

The neutron diffraction is measuring the differential scattering cross section. This can be converted to the structure factor \(S(Q)\). Using the PDFFourierTransform algorithm, one can obtain the pair distribution function, \(G(r)\):

(1)\[G(r)=\frac{2}{\pi}\int_0^\infty Q[S(Q)-1]\sin(Qr) dQ\]

One can transform between this quantity and \(GK(r)\) or \(g(r)\) using:

(2)\[GK(r)=\frac{\langle b_{coh} \rangle^2}{4\pi r\rho_0}G(r)\]

(3)\[g(r)=\frac{G(r)}{4\pi r\rho_0}+1\]

where \(\rho_0\) is the sample number density and \(\langle b_{coh} \rangle^2\) is defined in the Materials concept page.

NOTE: This algorithm requires that SetSampleMaterial v1 is called prior in order to determine the \(\rho_0\) and \(\langle b_{coh} \rangle^2\) terms.

PyStoG

This algorithm uses the external project PyStoG and specifically uses the pystog.converter.Converter object. To modify the underlying algorithms, the following functions are used for the conversions.

• \(G(r)\) conversions are:

  • To \(G_K(r)\) see pystog.converter.Converter.G_to_GK()

  • To \(g(r)\) see pystog.converter.Converter.G_to_g()

• \(G_K(r)\) conversions are:

  • To \(G(r)\) see pystog.converter.Converter.GK_to_G()

  • To \(g(r)\) see pystog.converter.Converter.GK_to_g()

• \(g(r)\) conversions are:

  • To \(G(r)\) see pystog.converter.Converter.g_to_G()

  • To \(GK(r)\) see pystog.converter.Converter.g_to_GK()

Usage

import wget
import numpy as np
import matplotlib.pyplot as plt
from mantid.simpleapi import CreateWorkspace
# Grab the real data for argon
url = "https://raw.githubusercontent.com/marshallmcdonnell/pystog/master/tests/test_data/argon.real_space.dat"
filename = wget.download(url)
r, gofr, GofR_, GKofR_ = np.loadtxt(filename, skiprows=2, unpack=True)

# Convert gofr to Mantid wksp
g_of_r = CreateWorkspace(DataX=r, DataY=gofr,
                         UnitX="Angstrom",
                         Distribution=True)
SetSampleMaterial(InputWorkspace=g_of_r, ChemicalFormula='Ar')
bigG_of_r=PDConvertRealSpace(InputWorkspace=g_of_r, From='g(r)', To='G(r)')
GK_of_r=PDConvertRealSpace(InputWorkspace=g_of_r, From='g(r)', To='GK(r)')

fig, ax = plt.subplots(subplot_kw={'projection':'mantid'})
ax.plot(g_of_r,'k-', label='$g(r)$')
ax.plot(bigG_of_r,'r-', label='$G(r)$')
ax.plot(GK_of_r,'b-', label='$G_K(r)$')
ax.legend() # show the legend
ax.set_xlabel('$r(\AA)$')
fig.show()

The output should look like:

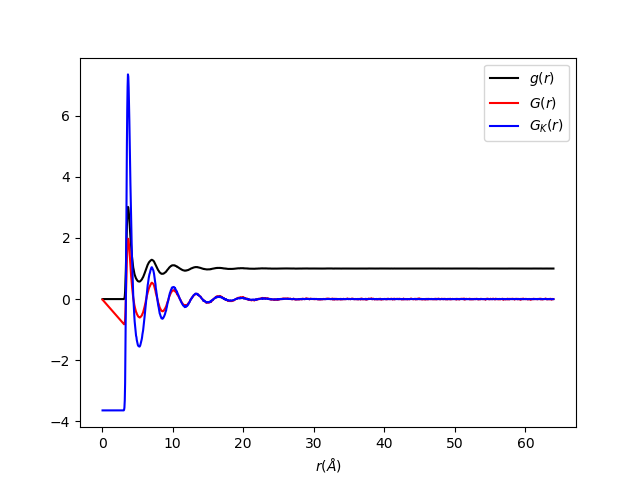
Categories: AlgorithmIndex | Diffraction\Utility

Source

Python: PDConvertRealSpace.py