\(\renewcommand\AA{\unicode{x212B}}\)

PawleyFit v1

Enable screenshots using DOCS_SCREENSHOTS in CMake

Summary

This algorithm performs a Pawley-fit on the supplied workspace.

See Also

PoldiPeakSearch

Properties

Name	Direction	Type	Default	Description
InputWorkspace	Input	MatrixWorkspace	Mandatory	Input workspace that contains the spectrum on which to perform the Pawley fit.
WorkspaceIndex	Input	number	0	Spectrum on which the fit should be performed.
StartX	Input	number	0	Lower border of fitted data range.
EndX	Input	number	0	Upper border of fitted data range.
LatticeSystem	Input	string	Triclinic	Lattice system to use for refinement. Allowed values: [‘Cubic’, ‘Tetragonal’, ‘Hexagonal’, ‘Rhombohedral’, ‘Orthorhombic’, ‘Monoclinic’, ‘Triclinic’]
InitialCell	Input	string	1.0 1.0 1.0 90.0 90.0 90.0	Specification of initial unit cell, given as ‘a, b, c, alpha, beta, gamma’.
PeakTable	Input	TableWorkspace	Mandatory	Table with peak information. Can be used instead of supplying a list of indices for better starting parameters.
RefineZeroShift	Input	boolean	False	If checked, a zero-shift with the same unit as the spectrum is refined.
PeakProfileFunction	Input	string	Gaussian	Profile function that is used for each peak. Allowed values: [‘AsymmetricPearsonVII’, ‘BackToBackExponential’, ‘Bk2BkExpConvPV’, ‘DeltaFunction’, ‘ElasticDiffRotDiscreteCircle’, ‘ElasticDiffSphere’, ‘ElasticIsoRotDiff’, ‘ExamplePeakFunction’, ‘Gaussian’, ‘IkedaCarpenterPV’, ‘Lorentzian’, ‘PseudoVoigt’, ‘Voigt’]
EnableChebyshevBackground	Input	boolean	False	If checked, a Chebyshev polynomial will be added to model the background.
ChebyshevBackgroundDegree	Input	number	0	Degree of the Chebyshev polynomial, if used as background.
CalculationOnly	Input	boolean	False	If enabled, no fit is performed, the function is only evaluated and output is generated.
OutputWorkspace	Output	MatrixWorkspace	Mandatory	Workspace that contains measured spectrum, calculated spectrum and difference curve.
RefinedCellTable	Output	TableWorkspace	Mandatory	TableWorkspace with refined lattice parameters, including errors.
RefinedPeakParameterTable	Output	TableWorkspace	Mandatory	TableWorkspace with refined peak parameters, including errors.
ReducedChiSquare	Output	number		Outputs the reduced chi square value as a measure for the quality of the fit.

Description

The algorithm performs a fit of lattice parameters using the principle approach described in a paper by Pawley [Pawley]. In this approach the reflection positions are calculated from lattice parameters and the reflection’s Miller indices (\(hkl\)), while the other profile parameters for each peak are freely refined.

PawleyFit requires a MatrixWorkspace with at least one spectrum in terms of either \(d\) or \(Q\), the index of the spectrum can be supplied to the algorithm as a parameter. Furthermore, the range which is used for refinement can be changed by setting the corresponding properties.

In addition, a TableWorkspace with information about the reflections that are found in the spectrum must be passed as well. There must be four columns with the captions “HKL”, “d”, “FWHM (rel.)” and “Intensity”. The HKL column can be supplied either as V3D or as a string with 3 numbers separated by space, comma or semi-colon and possibly surrounded by square brackets. One way to obtain such a table is to use three algorithms that are used in analysis of POLDI data, which produce tables in a suitable format. Details are given in the usage example section.

Along with the workspaces containing fit results and parameter values, the algorithm also outputs the reduced \(\chi^2\)-value, which is also written in the log.

Usage

Note

To run these usage examples please first download the usage data, and add these to your path. In Mantid this is done using Manage User Directories.

For the usage example there is a calculated, theoretical diffraction pattern (including a bit of noise) for Silicon, which crystallizes in space group \(Fd\overline{3}m\) and has a cubic cell with lattice parameter \(a=5.4311946\,\mathrm{\AA{}}\).

import numpy as np

# Load spectrum for Silicon in the d-range down to 0.7
si_spectrum = Load("PawleySilicon.nxs")

# In order to index the peaks later on, generate reflection for Si
Si = PoldiCreatePeaksFromCell(SpaceGroup='F d -3 m',
                              Atoms='Si 0 0 0 1.0 0.05',
                              a=5.43, LatticeSpacingMin=0.7)

print("Silicon has {} unique reflections with d > 0.7.".format(Si.rowCount()))

# Find peaks in the spectrum
si_peaks = PoldiPeakSearch(si_spectrum)

# Index the peaks, will generate a workspace named 'si_peaks_indexed_Si'
indexed = PoldiIndexKnownCompounds(si_peaks, CompoundWorkspaces='Si')

si_peaks_indexed = AnalysisDataService.retrieve('si_peaks_indexed_Si')

# 3 peaks have two possibilities for indexing, because their d-values are identical
print("The number of peaks that were indexed: {}".format(si_peaks_indexed.rowCount()))

# Run the actual fit with lattice parameters that are slightly off
si_fitted, si_cell, si_params, chi_square = PawleyFit(si_spectrum,
                      LatticeSystem='Cubic',
                      InitialCell='5.436 5.436 5.436',
                      PeakTable=si_peaks_indexed)

si_cell = AnalysisDataService.retrieve("si_cell")

a = np.round(si_cell.cell(0, 1), 6)
a_err = np.round(si_cell.cell(0, 2), 6)
a_diff = np.round(np.fabs(a - 5.4311946), 6)

print("The lattice parameter was refined to a = {} +/- {}".format(a, a_err))
print("The deviation from the actual parameter (a=5.4311946) is: {}".format(a_diff))
print("This difference corresponds to {:.2f} standard deviations.".format(np.round(a_diff / a_err, 2)))
print("The reduced chi square of the fit is: {:.2f}".format(np.round(chi_square, 3)))

Running this script will generate a bit of output about the results of the different steps. At the end the lattice parameter differs less than one standard deviation from the actual value.

Silicon has 18 unique reflections with d > 0.7.
The number of peaks that were indexed: 15
The lattice parameter was refined to a = 5.431205 +/- 1.6e-05
The deviation from the actual parameter (a=5.4311946) is: 1e-05
This difference corresponds to 0.63 standard deviations.
The reduced chi square of the fit is: 1.04

It’s important to check the output data, which is found in the workspace labeled si_fitted. Plotting it should show that the residuals are just containing background noise and no systematic deviations. Of course, depending on the sample and the measurement this will differ between cases.

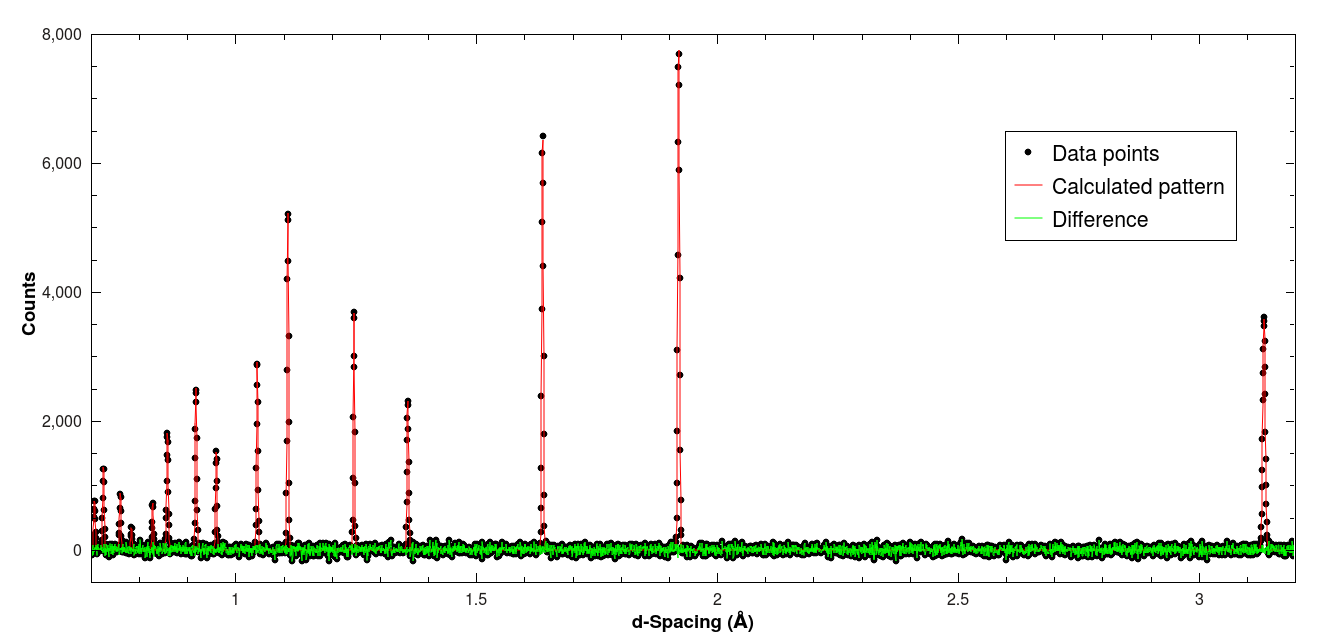
Result of the Pawley fit example with silicon.

[Pawley]

Pawley, G. S. “Unit-Cell Refinement from Powder Diffraction Scans.”, J. Appl. Crystallogr. 14, 1981, 357. doi:10.1107/S0021889881009618.

Categories: AlgorithmIndex | Diffraction\Fitting

Source

C++ header: PawleyFit.h

C++ source: PawleyFit.cpp