\(\renewcommand\AA{\unicode{x212B}}\)

ModeratorTzero v1

Summary

Corrects the time of flight of an indirect geometry instrument by a time offset that is dependent on the energy of the neutron after passing through the moderator.

See Also

ModeratorTzeroLinear

Properties

Name	Direction	Type	Default	Description
InputWorkspace	Input	MatrixWorkspace	Mandatory	The name of the input workspace, containing events and/or histogram data, in units of time-of-flight
OutputWorkspace	Output	MatrixWorkspace	Mandatory	The name of the output workspace
EMode	Input	string	Indirect	The energy mode (default: Indirect). Allowed values: [‘Indirect’, ‘Direct’, ‘Elastic’]
tolTOF	Input	number	0.1	Tolerance in the calculation of the emission time, in microseconds (default:1)
Niter	Input	m	1	Number of iterations (default:1)

Description

Corrects the time of flight (TOF) by a time offset that is dependent on the energy of the neutron after passing through the moderator. A heuristic formula for the correction is stored in the instrument definition file. Below is shown the entry in the instrument file for the VISION beamline:

<!-- formula for t0 calculation. See http://muparser.sourceforge.net/mup_features.html#idDef2 for available operators -->
<parameter name="t0_formula" type="string">
  <value val="(incidentEnergy < 34.7332) ? 37.011296*incidentEnergy^(-0.052874) : (incidentEnergy < 88.7556) ? 124.267307*incidentEnergy^(-0.394282) : (incidentEnergy < 252.471) ? 963.775145*incidentEnergy^(-0.850919) : (incidentEnergy < 420.145) ? 33.225834*incidentEnergy^(-0.242105) : (incidentEnergy < 100000.0) ? 120.569231*incidentEnergy^(-0.455477) : 0.0" />
</parameter>

The recorded \(TOF = t_0 + t_i + t_f\) with

• \(t_0\): emission time from the moderator

• \(t_1\): time from moderator to sample or monitor

• \(t_2\): time from sample to detector

This algorithm will replace \(TOF\) with \(TOF^* = TOF-t_0 = t_i+t_f\)

For a direct geometry instrument, the incident energy \(E_1\) is the same for all neutrons. Hence, the moderator emission time is the same for all neutrons. For an indirect geometry instrument, \(E_1\) is different for each neutron and is not known. However, the final energy \(E_2\) selected by the analyzers is known.

• \(t_0 = func(E_1)\) , a function of the incident energy

• \(t_1 = L_1/v_1\) with \(L_1\) the distance from moderator to sample, and \(v_1\) the initial unknown velocity (\(E_1=1/2*m*v_1^2\))

• \(t_2 = L_2/v_2\) with \(L_2\) the distance from sample to detector, and \(v_2\) is the final fixed velocity (\(E_2=1/2*m*v_2^2\))

Note

We obtain \(TOF^*\) as an iterative process, taking into account the fact that the correction \(t_0\) is much smaller than \(t_i+t_f\). Thus \(TOF-t_0^{(n)} = L_1/v_1^{(n)} + L_2/v_2\) , \(n=0, 1, 2,..\) Set \(t_0^{(0)}=0\) and obtain \(v_1^{(0)}\) from the previous formula. From \(v_1^{(0)}\) we obtain \(E_1^{(0)}\) Set \(t_0^{(1)}=func( E_1^{(0)} )\) and repeat the steps until \(|t_0^{(n+1)} - t_0^{(n+1)}| < tolTOF\). With \(tolTOF=0.1 microsecond\), only one iteration is needed for convergence.

Here’s the result of applying ModeratorTzero to both the event list and the histogrammed data of a run in the VISION beamline. The transformation of either events or histograms shifts the curve to smaller TOF’s. The transformed curves are not supposed to be identical, but similar and differentiated from the original curve.

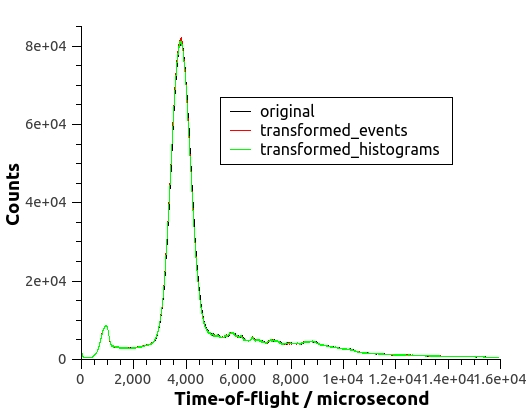
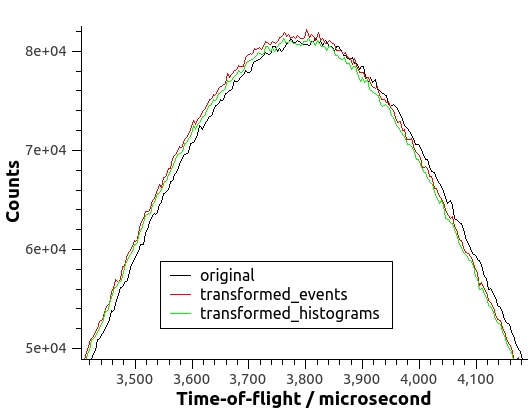
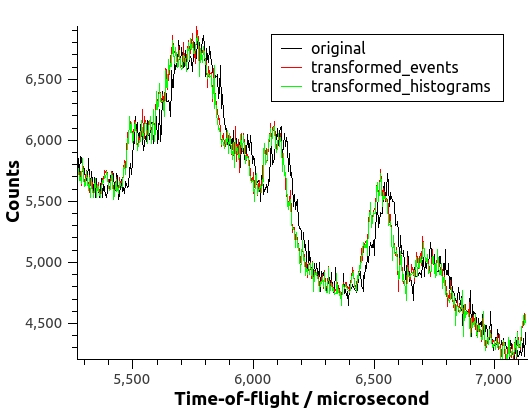
For indirect instruments featuring an incoming neutron flux having a sufficiently narrow distribution of energies, a linear relationship between \(t_0\) and the wavelength of the incoming neutron can be established. This relation allows for coding of an algorithm with faster execution times. For indirect instruments that comply with these conditions, use of ModeratorTzeroLinear v1 is preferred.

Categories: AlgorithmIndex | CorrectionFunctions\InstrumentCorrections

Source

C++ header: ModeratorTzero.h

C++ source: ModeratorTzero.cpp