\(\renewcommand\AA{\unicode{x212B}}\)

WienerSmooth v1

Summary

Smooth spectra using Wiener filter.

See Also

FFTSmooth

Properties

Name	Direction	Type	Default	Description
InputWorkspace	Input	MatrixWorkspace	Mandatory	An input workspace.
WorkspaceIndexList	Input	int list		Workspace indices for spectra to process. If empty smooth all spectra.
OutputWorkspace	Output	MatrixWorkspace	Mandatory	An output workspace.

Description

This algorithm smooths the data in a workspace using the Wiener filter method. The fiter is a function which if convolved with an input minimizes the noise in the output.

\[s_o(t) = \int_{-\infty}^\infty s_i(\tau) w(t-\tau) d\tau\]

For more detail see Wikipedia article http://en.wikipedia.org/wiki/Wiener_filter.

WienerSmooth uses the power spectrum of the input signal \(s_i\) to build the filter \(W(\nu)=\int_{-\infty}^\infty w(t)e^{-2\pi it\nu} dt\)

First the noise level is estimated from the higher frequencies of the power spectrum. Then the fiter function is constructed out of three pieces. The first piece is at the lower frequencies where the power spectrum is well above the noise. At this region the the filter function is calculated with the formula:

\[W(\nu) = \frac{1}{1+N/P(\nu)},\]

where \(P(\nu)\) is the power spectrum and \(N\) is the noise. The higher the power spectrum the closer the filter function to 1.

At the medium frequency range where the power spectrum is getting closer to the noise the filter is described with a piece of a sigmoid decreasing to about the noise level. After that all values are set to zero.

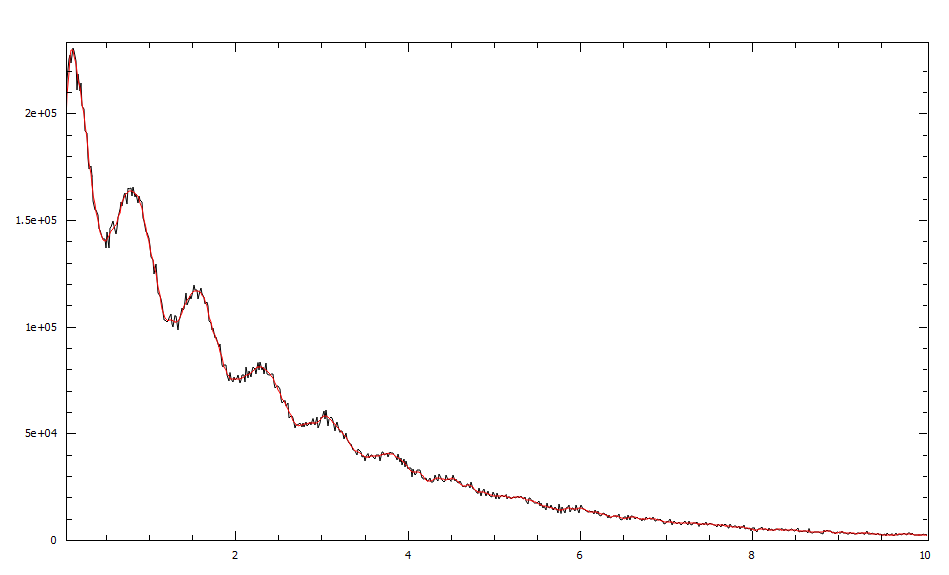
In this example the black curve is the input data and the red one is the result of smoothing.

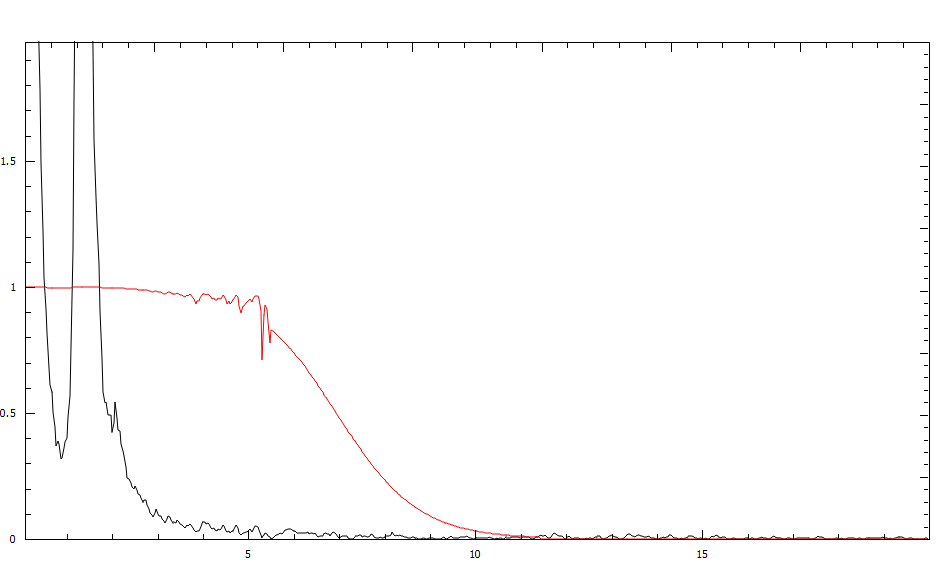
The image below shows the Wiener filter function used (red) along with the power spectrum of the data (black).

Usage

Example - Smooth noisy data

import random
import math

# Define a function
def fun(x):
    return math.sin(x) + x /10

# Create a workspace with noisy data.

# Size of the data set
n = 200

# Define the x-values
interval = (-10.0,10.0)
dx = (interval[1] - interval[0]) / (n - 1)
x = [interval[0] + dx * i for i in range(n)]

# Define the y-values as a function fun(x) + random noise
noise = 0.1
y = [fun(x[i]) +  random.normalvariate(0.0,noise) for i in range(n)]

# Create a workspace
ws = CreateWorkspace(x,y)

# Smooth the data using the Wiener filter
smooth = WienerSmooth(ws,0)

Categories: AlgorithmIndex | Arithmetic\FFT | Transforms\Smoothing

Source

C++ header: WienerSmooth.h

C++ source: WienerSmooth.cpp