Poisson Cost Function¶
Description¶
The Poisson cost function is designed to be applied to data, which has a low number of counts/events. In this scenario a fit is being performed using a model (function) to some low stats data.
The number of counts/events in bin \(i\) is given by \(y_i\) and the corresponding value for the model is \(\mu_i\). Where the values of \(y_i\) and \(\mu_i\) are strictly positive.
The quality of the fit can be represented numerically by the deviance (\(D\))
where the first two terms provide a measure for small variations between \(y_i\) and \(\mu_i\), whereas the third term provides a measure of large variations. Therefore, by minimizing the deviance the best fit can be identified. This method is also known as the Poisson deviance or Poisson log-linear model.
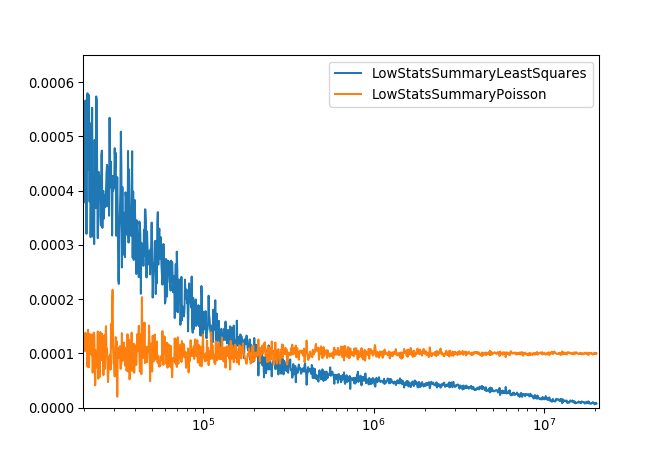
When performing a fit on Poisson distributed data care needs to be taken when selecting the cost function. For a large number of events/counts the least squares cost function can be used to minimize Poisson distributed data. This is because in the limit of large numbers of events/counts the Poisson and Gaussian distributions are approximately equal. In the limits of low events/counts using a least squares cost function can lead to biased results.
Example¶
Given a workspace with low counts, a fit can be done in a script as follows:
Fit(Function=f,InputWorkspace=workspace,Output="outputName",CreateOutput=True,CostFunction="Poisson",Minimizer="Levenberg-MarquardtMD")
The plot below demonstrates the difference between using the Poisson and Least Squares cost functions for a given parameter over a series of fits to data with different number of counts. The Poisson model gives a much more consistent result and means no special treatment is required for zero counts.
References¶
[1] Rodríguez, G. (2007). Lecture Notes on Generalized Linear Models.