\(\renewcommand\AA{\unicode{x212B}}\)

Meier

Description

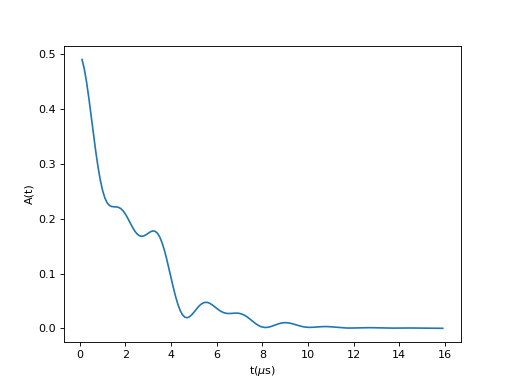
Time dependence of the polarization function for a static muon interacting with nuclear spin [1].

\[A(t)=\frac{A_0*G(t)*L(t)}{3}(2P_x+P_z)\]

where:

\[G(t) = e^{-0.5(\sigma t)^2},\]

\[L(t) = e^{-\Lambda t},\]

\[P_z(t) = \frac{1}{2J+1}\left\{1+\sum^J_{m=-J+1}[\cos^2(2\alpha_m)+\sin^2(2\alpha_m)\cos(\lambda^+_m-\lambda^-_m)t]\right\},\]

\[P_x(t) = \frac{1}{2J+1}\sum^J_{m=-J} \{ \cos^2\alpha_{m+1}\sin^2\alpha_m\cos(\lambda_{m+1}^+-\lambda_m^+)t +\cos^2\alpha_{m+1}\cos^2\alpha_m\cos(\lambda_{m+1}^+-\lambda_m^-)t +\sin^2\alpha_{m+1}\sin^2\alpha_m\cos(\lambda_{m+1}^--\lambda_m^+)t +\sin^2\alpha_{m+1}\cos^2\alpha_m\cos(\lambda_{m+1}^--\lambda_m^-)t\},\]

\[\lambda_m^\pm = \frac{1}{2}[\omega_Q(2m^2-2m+1)+\omega_D\pm W_m],\]

\[W_m = \{(\omega_D+\omega_Q)^2(2m-1)^2+\omega_D^2[J(J+1)-m(m-1)]\}^\frac{1}{2},\]

\[\tan(2\alpha_m)=\frac{\omega_D[J(J+1)-m(m-1)]^\frac{1}{2}}{(1-2m)(\omega_D+\omega_Q)},\]

\(A_0\) is the amplitude

\(\omega_D\) is the angular frequency due to dipolar coupling

\(\omega_Q\) is the angular frequency due to quadrupole interaction of the nuclear spin \(J\) due to a field gradient exerted by the presence of the muon

\(J\) is the total angular momentum quantum number

\(\sigma\) is the gaussian decay rate

\(\Lambda\) is the exponential decay rate

and \(m\) is the z-component of the total orbital quantum number.

(Source code, png, hires.png, pdf)

Attributes (non-fitting parameters)

Name	Type	Default	Description
Spin

References

[1] P.H. Meier, HFI 17-19 427-434 (1984).

Properties (fitting parameters)

Name	Default	Description
A0	0.5	Amplitude
FreqD	0.01	Angular Frequency due to dipolar coupling (MHz)
FreqQ	0.05	Angular Frequency due to quadrupole interaction of the nuclear spin (MHz) due to a field gradientexerted by the presence of the muon
Sigma	0.2	Gaussian decay rate
Lambda	0.1	Exponential decay rate

Categories: FitFunctions | Muon\MuonSpecific

Source

C++ header: Meier.h

C++ source: Meier.cpp