Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| LHSWorkspace | Input | MatrixWorkspace | Mandatory | LHS input workspace. |
| RHSWorkspace | Input | MatrixWorkspace | Mandatory | RHS input workspace. |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | Output stitched workspace. |
| StartOverlap | Input | number | Optional | Start overlap x-value in units of x-axis. Optional. |
| EndOverlap | Input | number | Optional | End overlap x-value in units of x-axis. Optional. |
| Params | Input | dbl list | Rebinning Parameters. See Rebin for format. If only a single value is provided, start and end are taken from input workspaces. | |
| ScaleRHSWorkspace | Input | boolean | True | Scaling either with respect to LHS workspace or RHS workspace |
| UseManualScaleFactor | Input | boolean | False | True to use a provided value for the scale factor. |
| ManualScaleFactor | Input | number | 1 | Provided value for the scale factor. Optional. |
| OutScaleFactor | Output | number | The actual used value for the scaling factor. |
Stitches single histogram Matrix Workspaces together outputting a stitched Matrix Workspace. Note that workspaces must be histogrammed, you may want to use ConvertToHistogram v1 on workspaces prior to passing them to this algorithm.
Either the right-hand-side or left-hand-side workspace can be chosen to be scaled. Users can optionally provide Rebin v1 Params, otherwise they are calculated from the input workspaces. Likewise, StartOverlap and EndOverlap are optional. If not provided, then these are taken to be the region of X-axis intersection.
The algorithm workflow is as follows:
Below is a flowchart illustrating the steps in the algorithm (it assumes ScaleRHSWorkspace is true). Figure on the left corresponds to the workflow when no scale factor is provided, while figure on the right corresponds to workflow with a manual scale factor specified by the user.
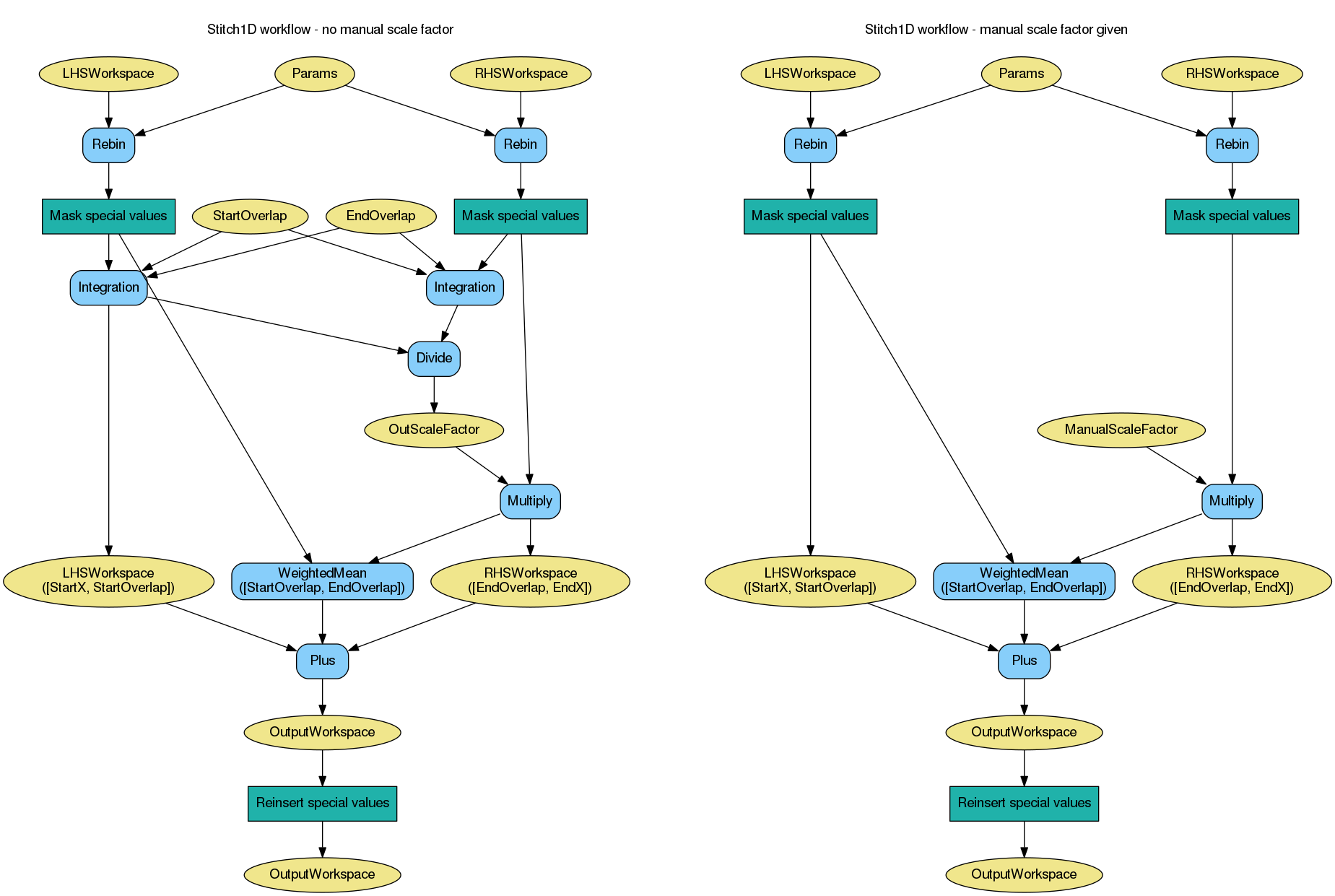
Errors are are handled and propagated in every step according to Error Propagation. This includes every child algorithm: Rebin v1, Integration v1, Divide v1, Multiply v1 and WeightedMean v1. In particular, when the scale factor is calculated as the quotient of the left-hand-side integral and the right-hand-side integral, the result is a number with an error associated, and therefore the multiplication of the right-hand-side workspace by this number takes into account its error.
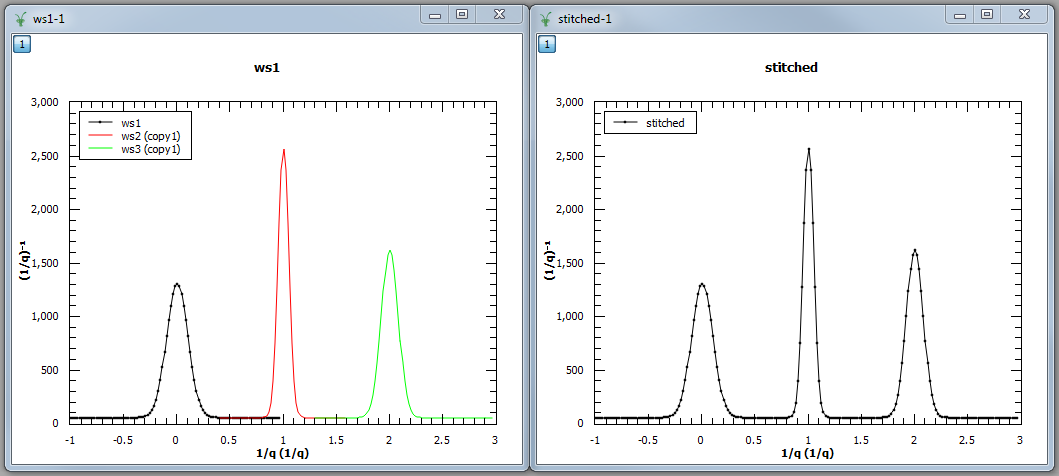
Example - a basic example using stitch1D to stitch two workspaces together.
import numpy as np
def gaussian(x, mu, sigma):
"""Creates a gaussian peak centered on mu and with width sigma."""
return (1/ sigma * np.sqrt(2 * np.pi)) * np.exp( - (x-mu)**2 / (2*sigma**2))
#create two histograms with a single peak in each one
x1 = np.arange(-1, 1, 0.02)
x2 = np.arange(0.4, 1.6, 0.02)
ws1 = CreateWorkspace(UnitX="1/q", DataX=x1, DataY=gaussian(x1[:-1], 0, 0.1)+1)
ws2 = CreateWorkspace(UnitX="1/q", DataX=x2, DataY=gaussian(x2[:-1], 1, 0.05)+1)
#stitch the histograms together
stitched, scale = Stitch1D(LHSWorkspace=ws1, RHSWorkspace=ws2, StartOverlap=0.4, EndOverlap=0.6, Params=0.02)
Output:
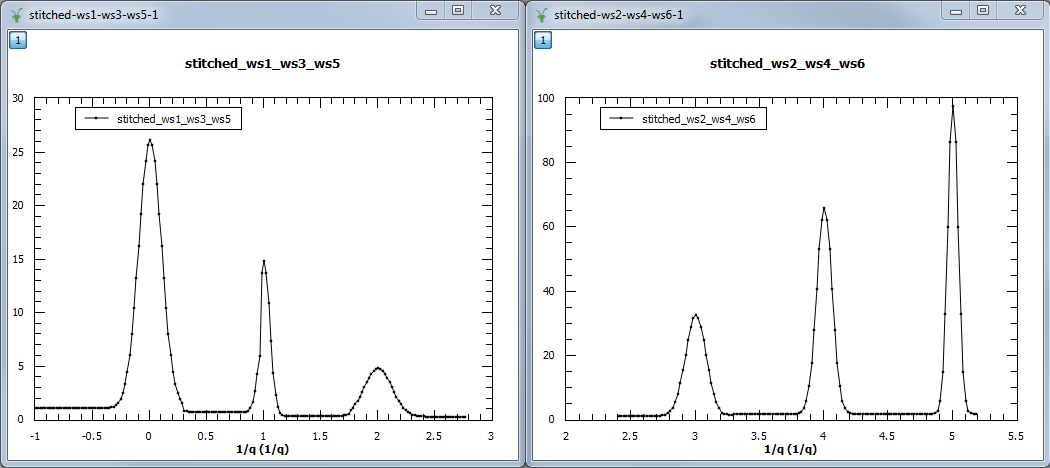
Example - a practical example using reflectometry data and a scale factor.
trans1 = Load('INTER00013463')
trans2 = Load('INTER00013464')
trans1_wav = CreateTransmissionWorkspaceAuto(trans1)
trans2_wav = CreateTransmissionWorkspaceAuto(trans2)
stitched_wav, y = Stitch1D(trans1_wav, trans2_wav, UseManualScaleFactor=True, ManualScaleFactor=0.85)
Output:
Categories: Algorithms | Reflectometry
C++ source: Stitch1D.cpp (last modified: 2018-03-07)
C++ header: Stitch1D.h (last modified: 2018-03-07)