Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspaces | Input | str list | Mandatory | Input Workspaces. List of histogram workspaces to stitch together. At least 2 workspaces must be supplied for stitching and all must be either Matrix Workspaces or Workspace Groups containing Matrix Workspaces only. |
| OutputWorkspace | Output | Workspace | Mandatory | Output stitched workspace. |
| Params | Input | dbl list | Mandatory | Rebinning Parameters. See Rebin for format. |
| StartOverlaps | Input | dbl list | Start overlaps for stitched workspaces. If specified, the number of StartOverlaps must be 1 less than the number of input workspaces. Optional. | |
| EndOverlaps | Input | dbl list | End overlaps for stitched workspaces. If specified, the number of EndOverlaps must be the same as the number of StartOverlaps. Optional. | |
| ScaleRHSWorkspace | Input | boolean | True | Scaling either with respect to workspace 1 or workspace 2 |
| UseManualScaleFactors | Input | boolean | False | True to use provided values for the scale factor. |
| ManualScaleFactors | Input | dbl list | Provided values for the scale factors. If specified, the number of ManualScaleFactors must either be one (in which case the provided value is applied to all input workspaces) or 1 less than the number of input workspaces | |
| OutScaleFactors | Output | dbl list | The actual used values for the scaling factors at each stitch step. | |
| ScaleFactorFromPeriod | Input | number | 1 | Provided index of period to obtain scale factor from. Periods are indexed from 1. Used only if stitching group workspaces, UseManualScaleFactors is true and ManualScaleFactors is set to default. |
Stitches single histogram Matrix Workspaces together outputting a stitched Matrix Workspace. This algorithm is a wrapper over Stitch1D v3.
The workspaces must be histogrammed. Use ConvertToHistogram v1 on workspaces prior to passing them to this algorithm.
The algorithm expects pairs of StartOverlaps and EndOverlaps values. The order in which these are provided determines the pairing. There should be N entries in each of these lists, where N = 1 - (No. of workspaces to stitch). StartOverlaps and EndOverlaps are in the same units as the X-axis for the workspace and are optional. For each pair of these values, the StartOverlaps value cannot exceed its corresponding EndOverlaps value. Furthermore, if either the start or end value is outside the range of X-axis intersection, they will be forcibly changed to the intersection min and max respectively.
This algorithm is also capable of stitching together matrix workspaces from multiple workspace groups. In this case, each group must contain the same number of workspaces. The algorithm will stitch together the workspaces in the first group before stitching workspaces from the next group on top of the previous ones.
When stitching the workspaces, either the RHS or LHS workspaces can be scaled. We can specify manual scale factors to use by setting UseManualScaleFactors true and passing values to ManualScaleFactors. For group workspaces, we can also use ScaleFactorFromPeriod to select a period which will obtain a vector of scale factors from the selected period. These scale factors are then applied to all other periods when stitching.
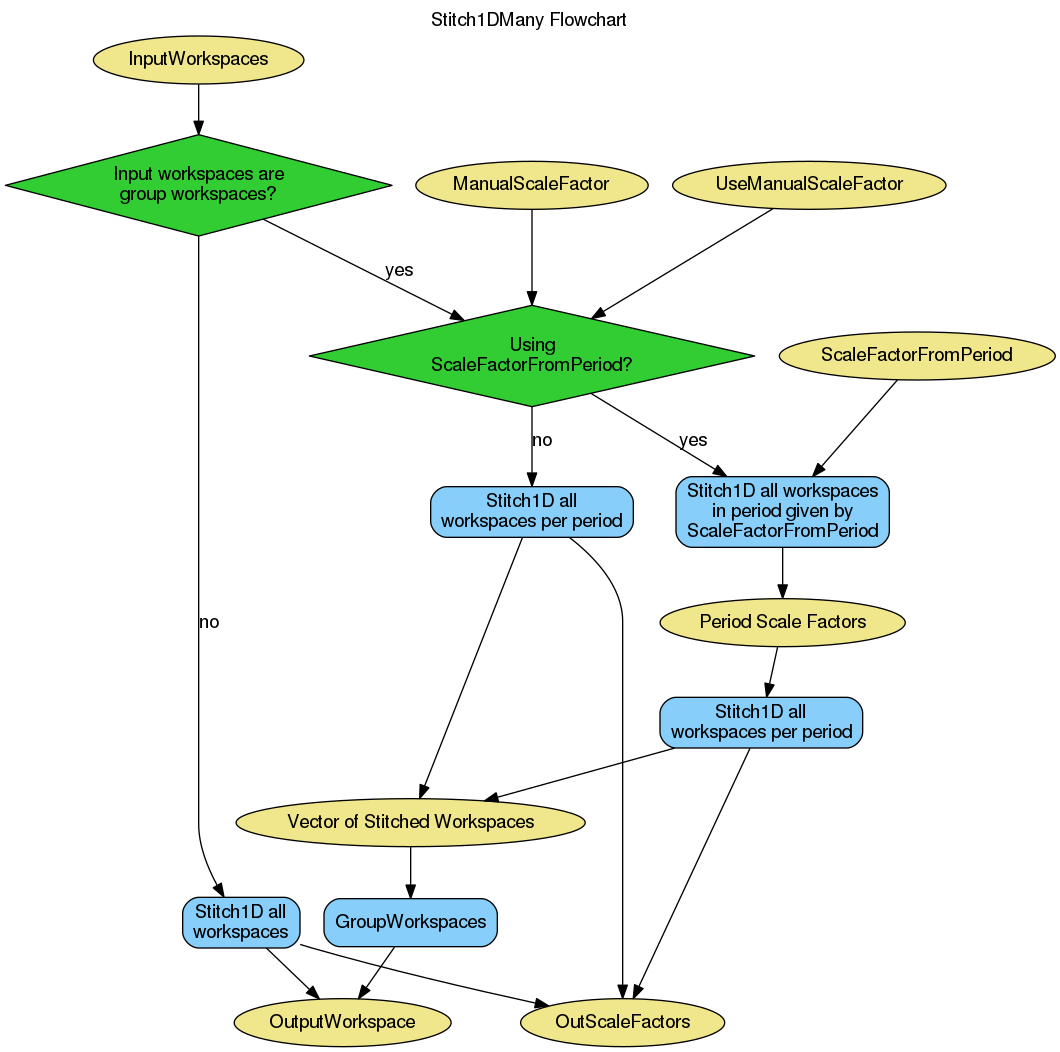
The algorithm workflow is as follows:
In the diagram below, all input parameters other than InputWorkspaces, UseManualScaleFactors, ManualScaleFactors and ScaleFactorFromPeriod have been omitted as they do not serve any purpose other than to be passed to the Stitch1DMany algorithm.
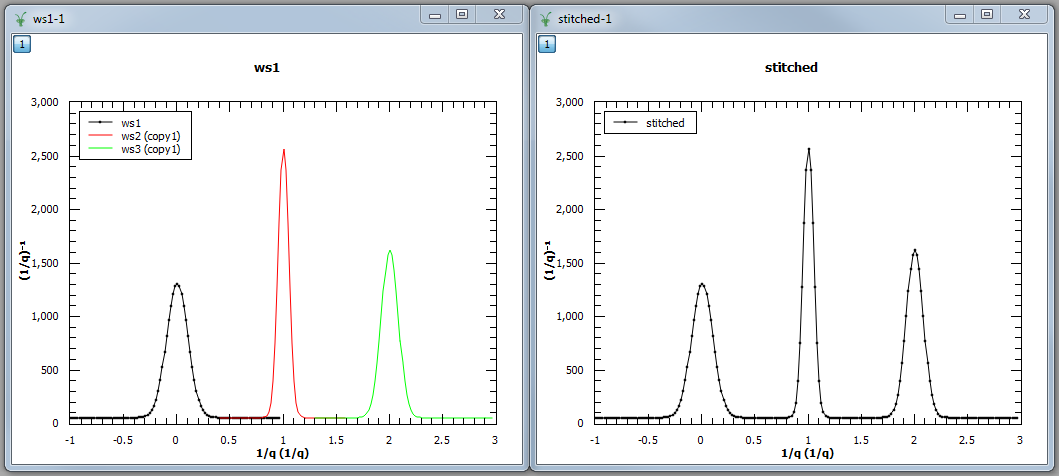
Example - a basic example using Stitch1DMany to stitch three workspaces together.
import numpy as np
def gaussian(x, mu, sigma):
"""Creates a gaussian peak centered on mu and with width sigma."""
return (1/ sigma * np.sqrt(2 * np.pi)) * np.exp( - (x-mu)**2 / (2*sigma**2))
# Create three histograms with a single peak in each one
x1 = np.arange(-1, 1, 0.02)
x2 = np.arange(0.4, 1.6, 0.02)
x3 = np.arange(1.3, 3, 0.02)
ws1 = CreateWorkspace(UnitX="1/q", DataX=x1, DataY=gaussian(x1[:-1], 0, 0.1)+1)
ws2 = CreateWorkspace(UnitX="1/q", DataX=x2, DataY=gaussian(x2[:-1], 1, 0.05)+1)
ws3 = CreateWorkspace(UnitX="1/q", DataX=x3, DataY=gaussian(x3[:-1], 2, 0.08)+1)
# Stitch the histograms together
workspaces = ws1.name() + "," + ws2.name() + "," + ws3.name()
stitched, scale = Stitch1DMany(InputWorkspaces=workspaces, StartOverlaps=[0.4, 1.2], EndOverlaps=[0.6, 1.4], Params=[0.02])
Output:
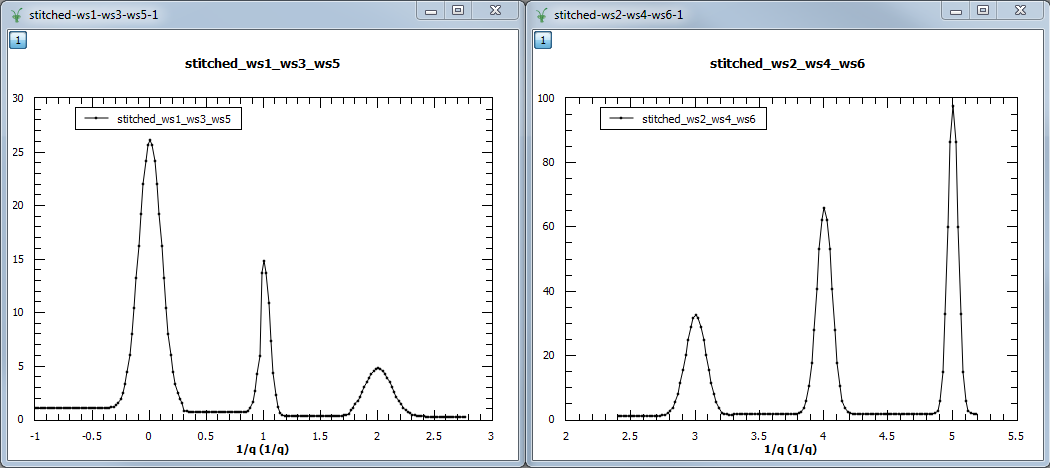
Example - another example using three group workspaces of two workspaces each.
import numpy as np
def gaussian(x, mu, sigma):
"""Creates a gaussian peak centered on mu and with width sigma."""
return (1/ sigma * np.sqrt(2 * np.pi)) * np.exp( - (x-mu)**2 / (2*sigma**2))
# Create six histograms with a single peak in each one
x1 = np.arange(-1, 1, 0.02)
x3 = np.arange(0.3, 1.8, 0.02)
x5 = np.arange(1.4, 2.8, 0.02)
x2 = np.arange(2.4, 3.5, 0.02)
x4 = np.arange(3.2, 4.9, 0.02)
x6 = np.arange(4.5, 5.2, 0.02)
ws1 = CreateWorkspace(UnitX="1/q", DataX=x1, DataY=gaussian(x1[:-1], 0, 0.1)+1)
ws3 = CreateWorkspace(UnitX="1/q", DataX=x3, DataY=gaussian(x3[:-1], 1, 0.05)+1)
ws5 = CreateWorkspace(UnitX="1/q", DataX=x5, DataY=gaussian(x5[:-1], 2, 0.12)+1)
ws2 = CreateWorkspace(UnitX="1/q", DataX=x2, DataY=gaussian(x2[:-1], 3, 0.08)+1)
ws4 = CreateWorkspace(UnitX="1/q", DataX=x4, DataY=gaussian(x4[:-1], 4, 0.06)+1)
ws6 = CreateWorkspace(UnitX="1/q", DataX=x6, DataY=gaussian(x6[:-1], 5, 0.04)+1)
# Group first, second and third pairs of workspaces
groupWSNames1 = ws1.name() + "," + ws2.name()
gws1 = GroupWorkspaces(InputWorkspaces=groupWSNames1)
groupWSNames2 = ws3.name() + "," + ws4.name()
gws2 = GroupWorkspaces(InputWorkspaces=groupWSNames2)
groupWSNames3 = ws5.name() + "," + ws6.name()
gws3 = GroupWorkspaces(InputWorkspaces=groupWSNames3)
# Stitch together workspaces from each group
workspaceNames = gws1.name() + "," + gws2.name() + "," + gws3.name()
stitched, scale = Stitch1DMany(InputWorkspaces=workspaceNames, StartOverlaps=[0.3, 1.4], EndOverlaps=[3.3, 4.6], Params=[0.02])
Output:
Categories: Algorithms | Reflectometry
C++ source: Stitch1DMany.cpp (last modified: 2018-03-07)
C++ header: Stitch1DMany.h (last modified: 2018-03-07)