Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | An input workspace. |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | An output workspace. |
| Temperature | Input | string | SampleLog variable name that contains the temperature, or a number |
The fluctuation dissipation theorem [1,2] relates the dynamic susceptibility to the scattering function
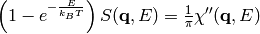
where 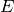 is the energy transfer to the system. The algorithm
assumes that the y axis of the input workspace contains the scattering
function
is the energy transfer to the system. The algorithm
assumes that the y axis of the input workspace contains the scattering
function  . The y axis of the output workspace will contain the
dynamic susceptibility. The temperature is extracted from a log attached
to the workspace, as the mean value. Alternatively, the temperature can
be directly specified. The algorithm will fail if neither option is
valid.
. The y axis of the output workspace will contain the
dynamic susceptibility. The temperature is extracted from a log attached
to the workspace, as the mean value. Alternatively, the temperature can
be directly specified. The algorithm will fail if neither option is
valid.
[1] S. W. Lovesey - Theory of Neutron Scattering from Condensed Matter, vol 1
[2] I. A. Zaliznyak and S. H. Lee - Magnetic Neutron Scattering in “Modern techniques for characterizing magnetic materials”
Example - Run Applied Detailed Balance
ws = CreateWorkspace(DataX='-5,-4,-3,-2,-1,0,1,2,3,4,5',DataY='2,2,2,2,2,2,2,2,2,2',DataE='1,1,1,1,1,1,1,1,1,1',UnitX='DeltaE')
ows = ApplyDetailedBalance(InputWorkspace='ws',OutputWorkspace='ows',Temperature='100')
print "The Y values in the Output Workspace are"
print str(ows.readY(0)[0:5])
print str(ows.readY(0)[5:10])
Output:
The Y values in the Output Workspace are
[-4.30861792 -3.14812682 -2.11478496 -1.19466121 -0.37535083]
[ 0.35419179 1.00380206 1.58223777 2.09729717 2.55592407]
Categories: Algorithms | Inelastic