Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | An input MatrixWorkspace. |
| BankNumbers | Input | int list | A list of the bank numbers to convert. If empty, will use all banksMust have at least one entry. | |
| SplitInto | Input | int list | 2 | A comma separated list of into how many sub-grid elements each dimension should split; or just one to split into the same number for all dimensions. Default 2. |
| SplitThreshold | Input | number | 200 | How many events in a box before it should be split. Default 200. |
| MaxRecursionDepth | Input | number | 20 | How many levels of box splitting recursion are allowed. The smallest box will have each side length 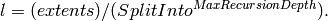 Default 20. Default 20. |
| OutputWorkspace | Output | MDEventWorkspace | Mandatory | Name of the output MDEventWorkspace. |
This algorithm takes a a MatrixWorkspace and converts it into a MDEventWorkspace that can be viewed in the SliceViewer.
The algorithm currently only works for instruments with rectangular detectors. The coordinates of the output workspace are:
Each MDEvent created has a weight given by the number of counts in that bin. Zero bins are not converted to events (saving memory).
Once created, the MDEventWorkspace can be viewed in the SliceViewer. It can also be rebinned with different parameters using BinMD v1. This allows you to view the data in detector-space. For example, you might use this feature to look at your detector’s sensitivity as a function of position, as well as a function of TOF. You can also do line plots of the data. See this screenshot for example:
If your instrument has several rectangular detectors, you can use the BankNumbers property to specify which one(s) to convert. The algorithm looks for rectangular detectors with the name ‘bankXX’ where XX is the bank number.
If you specify more than one bank number, then the algorithm will create a 4D MDEventWorkspace. The fourth dimension will be equal to the bank number, allowing you to easily pick a bank to view.
Categories: Algorithms | MDAlgorithms