Table of Contents
== Deprecation notice == Instead of using this algorithm to fit a Lorentzian please use the Fit algorithm where the Function parameter of this algorithm is used to specified the fitting function, including selecting a Lorentzian.
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | Name of the input Workspace |
| WorkspaceIndex | Input | number | 0 | The Workspace to fit, uses the workspace numbering of the spectra (default 0) |
| StartX | Input | number | Optional | A value of x in, or on the low x boundary of, the first bin to include in the fit (default lowest value of x) |
| EndX | Input | number | Optional | A value in, or on the high x boundary of, the last bin the fitting range (default the highest value of x) |
| BG0 | InOut | number | 0 | Constant background value (default 0) |
| BG1 | InOut | number | 0 | Linear background modelling parameter (default 0) |
| Height | InOut | number | 0 | height of peak (not the height may be refined to a negative value to fit a dipped curve) |
| PeakCentre | InOut | number | 0 | Centre of peak (default 0) |
| HWHM | InOut | number | 1 | half-width at half-maximum (default 1) |
| Fix | Input | string | A list of comma separated parameter names which should be fixed in the fit | |
| MaxIterations | Input | number | 500 | Stop after this number of iterations if a good fit is not found |
| OutputStatus | Output | string | ||
| OutputChi2overDoF | Output | number | ||
| Output | Input | string | If not empty OutputParameters TableWorksace and OutputWorkspace will be created. |
Takes a histogram in a 2D workspace and fit it to a Lorentzian function, i.e. to the function:
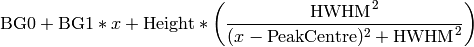
where
Note that the FWHM (Full Width Half Maximum) equals two times HWHM, and
the integral over the Lorentzian equals
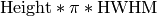 (ignoring the linear
background). In the literature you may also often see the notation
(ignoring the linear
background). In the literature you may also often see the notation
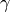 = HWHM.
= HWHM.
The figure below illustrate this symmetric peakshape function fitted to a TOF peak:
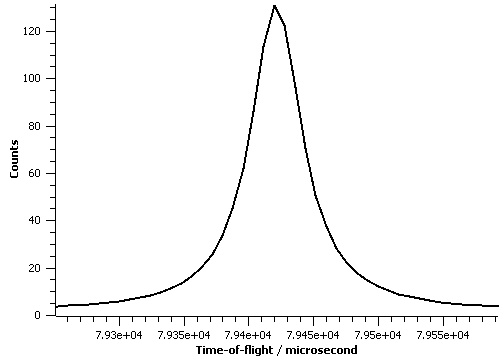
LorentzianWithConstBackground.png
Categories: Algorithms | Optimization | FitAlgorithms