3.5

PDFFourierTransform v1

../_images/PDFFourierTransform-v1_dlg.png

PDFFourierTransform dialog.

Summary

Fourier transform from S(Q) to G(r), which is paired distribution function (PDF). G(r) will be stored in another named workspace.

Properties

Name Direction Type Default Description
InputWorkspace Input MatrixWorkspace Mandatory S(Q), S(Q)-1, or Q[S(Q)-1]
OutputWorkspace Output MatrixWorkspace Mandatory Result paired-distribution function
InputSofQType Input string S(Q) To identify whether input function. Allowed values: [‘S(Q)’, ‘S(Q)-1’, ‘Q[S(Q)-1]’]
Qmin Input number Optional Minimum Q in S(Q) to calculate in Fourier transform (optional).
Qmax Input number Optional Maximum Q in S(Q) to calculate in Fourier transform. (optional)
Filter Input boolean False Set to apply Lorch function filter to the input
PDFType Input string G(r) Type of output PDF including G(r). Allowed values: [‘G(r)’, ‘g(r)’, ‘RDF(r)’]
DeltaR Input number Optional Step size of r of G(r) to calculate. Default = 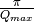\frac{\pi}{Q_{max}}.
Rmax Input number 20 Maximum r for G(r) to calculate.
rho0 Input number Optional Average number density used for g(r) and RDF(r) conversions (optional)

Description

The algorithm transforms a single spectrum workspace containing spectral density 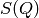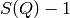S(Q), S(Q)-1, or Q[S(Q)-1] (as a fuction of MomentumTransfer or dSpacing units ) to a PDF (pair distribution function) as described below.

The input Workspace spectrum should be in the Q-space (MomentumTransfer) units . (d-spacing is not supported any more. Contact development team to fix that and enable dSpacing again)

Output Options:

G(r)

G(r) = 4\pi r[\rho(r)-\rho_0] = \frac{2}{\pi} \int_{0}^{\infty} Q[S(Q)-1]\sin(Qr)dQ

and in this algorithm, it is implemented as

G(r) = \frac{2}{\pi} \sum_{Q_{min}}^{Q_{max}} Q[S(Q)-1]\sin(Qr) M(Q,Q_{max}) \Delta Q

where M(Q,Q_{max}) is an optional filter function. If Filter property is set (true) then

M(Q,Q_{max}) = \frac{\sin(\pi Q/Q_{max})}{\pi Q/Q_{max}}

otherwise

M(Q,Q_{max}) = 1\,

g(r)

G(r) = 4 \pi \rho_0 r [g(r)-1]

transforms to

g(r) = \frac{G(r)}{4 \pi \rho_0 r} + 1

RDF(r)

RDF(r) = 4 \pi \rho_0 r^2 g(r)

transforms to

RDF(r) = r G(r) + 4 \pi \rho_0 r^2

Note: All output forms except G(r) are calculated by transforming G(r).

Usage

Example - PDF transformation examples:

# Simulates Load of a workspace with all necessary parameters #################
import numpy as np;
xx= np.array(range(0,100))*0.1
yy = np.exp(-((xx)/.5)**2)
ws=CreateWorkspace(DataX=xx,DataY=yy,UnitX='MomentumTransfer')
Rt= PDFFourierTransform(ws,InputSofQType='S(Q)',PDFType='g(r)');
#
# Look at sample results:
print 'part of S(Q) and its correlation function'
for i in xrange(0,10):
   print '! {0:4.2f} ! {1:5f} ! {2:f} ! {3:5f} !'.format(xx[i],yy[i],Rt.readX(0)[i],Rt.readY(0)[i])

Output:

part of S(Q) and its correlation function
! 0.00 ! 1.000000 ! 0.317333 ! -3.977330 !
! 0.10 ! 0.960789 ! 0.634665 ! 2.247452 !
! 0.20 ! 0.852144 ! 0.951998 ! 0.449677 !
! 0.30 ! 0.697676 ! 1.269330 ! 1.313403 !
! 0.40 ! 0.527292 ! 1.586663 ! 0.803594 !
! 0.50 ! 0.367879 ! 1.903996 ! 1.140167 !
! 0.60 ! 0.236928 ! 2.221328 ! 0.900836 !
! 0.70 ! 0.140858 ! 2.538661 ! 1.079278 !
! 0.80 ! 0.077305 ! 2.855993 ! 0.940616 !
! 0.90 ! 0.039164 ! 3.173326 ! 1.050882 !

Categories: Algorithms | Diffraction