Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | TableWorkspace | Mandatory | Workspace that contains unindexed peaks. |
| CompoundWorkspaces | Input | str list | A comma-separated list of workspace names or a workspace group. Each workspace must contain a list of indexed reflections. | |
| Tolerances | Input | dbl list | 0.01 | Maximum relative tolerance delta(d)/d for lines to be indexed. Either one value or one for each compound. |
| ScatteringContributions | Input | dbl list | 1 | Approximate scattering contribution ratio of the compounds. If omitted, all are assumed to contribute to scattering equally. |
| OutputWorkspace | Output | WorkspaceGroup | Mandatory | A workspace group that contains workspaces with indexed and unindexed reflections from the input workspace. |
In many experiments at POLDI it is well known which compounds are present in a sample, as well as their unit cells. For some algorithms it is necessary to index the peaks found in the correlation spectrum obtained by PoldiAutoCorrelation v5. This algorithm tries to index those peaks using lists of calculated reflections of one or more compounds (created with PoldiCreatePeaksFromCell v1). This technique is sometimes referred to as “pattern matching”. This implementation allows for a certain tolerance by allowing the user to specify an expected relative deviation of the lattice parameters, 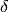 .
.
The major difficulty arises from the fact that typical POLDI experiments involve lattice deformations, which causes a shift in peak positions. For a single phase material with few peaks, this can be handled by making the tolerance larger - but only to a certain degree. If cell parameters are too large and consequently lattice plane spacings at low d-values too narrow, the indexing becomes ambiguous. Of course, introducing additional phases makes this situation even worse, leading to even more ambiguity.
To resolve these ambiguities, this algorithm assumes that a peak must occur somewhere in the vicinity of the theoretical position. As the distance between measured and calculated position grows, it becomes less and less likely that the measured peak corresponds to the theoretical one. By assuming a normal distribution centered at 0 and a standard deviation corresponding to an acceptable tolerance, the probability of finding the peak within this distance can be calculated.
The standard deviation 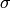 of the distribution is simply
of the distribution is simply 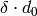 . To determine whether a peak can be indexed by a reflection, the algorithm checks if observed and calculated position are closer than
. To determine whether a peak can be indexed by a reflection, the algorithm checks if observed and calculated position are closer than 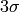 . If
. If 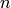 reflections are closer to an observed peak at position
reflections are closer to an observed peak at position 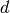 , all are considered a candidate for correct assignment. In order to decide which reflection is most likely to be correct, the probability is calculated for each combination of measured and calculated position and the candidate with highest value is used to indexed the measured peak.
, all are considered a candidate for correct assignment. In order to decide which reflection is most likely to be correct, the probability is calculated for each combination of measured and calculated position and the candidate with highest value is used to indexed the measured peak.
In the previous example, all calculated reflections get the same weight, that’s why the closest peak is always selected. This works for a single phase material, but it becomes error prone when more phases are present. A common example is the presence of a minority phase which makes up only a few percent of the sample, so that only very strong reflections of that compound can be detected. In that case a reflection of the minority compound may be very close the measured peak position, but in fact it may not even be detectable because of the low scattering contribution.
For that reason it’s possible to provide estimates for scattering contributions of each phase, which are used to calculate 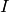 . Picking up the numbers from above,
. Picking up the numbers from above, 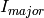 would be 0.95 and
would be 0.95 and  0.05. This means that reflections of the majority phase are assigned with higher priority, because it is much more likely to detect them. Since
0.05. This means that reflections of the majority phase are assigned with higher priority, because it is much more likely to detect them. Since 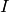 is proportional to
is proportional to 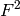 , the structure factors are also taken into account (including multiplicity related to the Laue class).
, the structure factors are also taken into account (including multiplicity related to the Laue class).
The output of the algorithm is a WorkspaceGroup, with one TableWorkspace for each input component containing the indexed peaks for that compound. Additionally there is a TableWorkspace with peaks that could not be indexed.
Note
To run these usage examples please first download the usage data, and add these to your path. In MantidPlot this is done using Manage User Directories.
The following example extracts peaks from the correlation spectrum of a Silicon standard measurement and indexes the observed peaks with Silicon reflections. One peak can not be indexed, but closer inspection of the correlation spectrum reveals that there is indeed no peak at this position (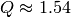 ).
).
# Load data file and instrument, perform correlation analysis
raw_6904 = LoadSINQFile(Filename = "poldi2013n006904.hdf", Instrument = "POLDI")
LoadInstrument(raw_6904, InstrumentName = "POLDI")
correlated_6904 = PoldiAutoCorrelation(raw_6904)
peaks_6904 = PoldiPeakSearch(correlated_6904)
PoldiFitPeaks1D(InputWorkspace = correlated_6904, FwhmMultiples = 4.0,
PeakFunction = "Gaussian", PoldiPeakTable = peaks_6904,
OutputWorkspace = "peaks_refined_6904",
FitPlotsWorkspace = "fit_plots_6904")
# Create theoretical reflections for Silicon
Si = PoldiCreatePeaksFromCell(SpaceGroup="F d -3 m",
Atoms="Si 0.0 0.0 0.0 1.0 0.005",
a=5.43071,
LatticeSpacingMin=0.7, LatticeSpacingMax=10.0)
# Index reflections
PoldiIndexKnownCompounds(InputWorkspace="peaks_refined_6904",
CompoundWorkspaces="Si",
Tolerances="0.005",
ScatteringContributions="1.0",
OutputWorkspace="Indexed")
print "Indexed_Si contains", mtd['peaks_refined_6904_indexed_Si'].rowCount(), "indexed peaks."
print "Number of unindexed peaks:", mtd['peaks_refined_6904_unindexed'].rowCount()
Output:
Indexed_Si contains 13 indexed peaks.
Number of unindexed peaks: 0
Categories: Algorithms | SINQ | Poldi