This fitting function models the dynamics structure factor of a particle undergoing discrete jumps on N-sites evenly distributed in a circle. The particle can only jump to neighboring sites. This is the most common type of discrete rotational diffusion in a circle.
Markov model for jumps between neighboring sites:
![\frac{d}{dt} p_j(t) = \frac{1}{\tau} [p_{j-1}(t) -2 p_j(t) + p_{j+1}(t)]](../_images/math/16f76033401e46030060e0347366e56726baa2e7.png)
The Decay fitting parameter 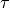 is the inverse of the
transition rate. This, along with the circle radius
is the inverse of the
transition rate. This, along with the circle radius  , conform
the two fundamental fitting parameters of the structure factor
, conform
the two fundamental fitting parameters of the structure factor
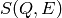 :
:
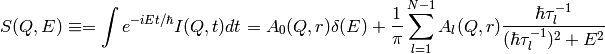
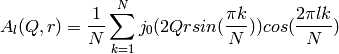
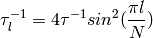
The transition rate, expressed in units of energy is 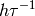 ,
with h = 4.135665616 meV THz.
,
with h = 4.135665616 meV THz.
When using InelasticDiffRotDiscreteCircle, he value of Q can be obained either though the Q attribute or can be calucated from the input workspace using the WorkspaceIndex property. The value calculated using the workspace is used whenever the Q attibute is empty.
Methyl Rotations can be modelled setting N=3. In this case, the inelastic part reduces to a single Lorentzian:
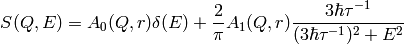
If, alternatively, one models these dynamics using the Lorentzian function provided in Mantid:
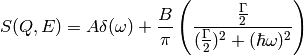
Then:
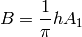
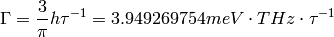
| Name | Type | Default | Description |
|---|---|---|---|
| N | |||
| NumDeriv | |||
| Q |
| Name | Default | Description |
|---|---|---|
| f0.Height | 1.0 | Scaling factor to be applied to the resolution. |
| f0.Centre | 0.0 | Shift along the x-axis to be applied to the resolution. |
| f0.Radius | 1.0 | Circle radius [Angstroms] |
| Intensity | 1.0 | scaling factor [arbitrary units] |
| Radius | 1.0 | Circle radius [Angstroms] |
| Decay | 1.0 | Inverse of transition rate, in nanoseconds if energy in micro-ev, or picoseconds if energy in mili-eV |
| Shift | 0.0 | Shift in domain |
Categories: FitFunctions | QuasiElastic