This fitting function models the dynamics structure factor of a particle undergoing continuous diffusion but confined to a spherical volume. According to Volino and Dianoux 1,
![S(Q,E\equiv \hbar \omega) = A_{0,0}(Q\cdot R) \delta (\omega) + \frac{1}{\pi} \sum_{l=1}^{N-1} (2l+1) A_{n,l} (Q\cdot R) \frac{x_{n,l}^2 D/R^2}{[x_{n,l}^2 D/R^2]^21+\omega^2}](../_images/math/4daed38eb9cf7c4fcf842a709eb5e76d4cad76c9.png)
![A_{n,l} = \frac{6x_{n,l}^2}{x_{n,l}^2-l(l+1)} [\frac{QRj_{l+1}(QR) - lj_l(QR)}{(QR)^2 - x_{n,l}^2}]^2](../_images/math/cb26e1496d6c83b62a8f27bb485bf90d2366691b.png)
Because of the spherical symmetry of the problem, the structure factor
is expressed in terms of the 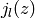 spherical Bessel functions.
Furthermore, the requirement that no particle flux can escape the sphere
leads to the following boundary
condition2:
spherical Bessel functions.
Furthermore, the requirement that no particle flux can escape the sphere
leads to the following boundary
condition2:
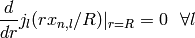
The roots of this set of equations are the numerical coefficients
 .
.
The fit function DiffSphere has an elastic part, modelled by fitting function ElasticDiffSphere and an inelastic part, modelled by InelasticDiffSphere.
When using InelasticDiffSphere, he value of Q can be obained either though the Q attribute or can be calucated from the input workspace using the WorkspaceIndex property. The value calculated using the workspace is used whenever the Q attibute is empty.
| Name | Type | Default | Description |
|---|---|---|---|
| NumDeriv | |||
| Q |
| Name | Default | Description |
|---|---|---|
| f0.Height | 1.0 | Scaling factor to be applied to the resolution. |
| f0.Centre | 0.0 | Shift along the x-axis to be applied to the resolution. |
| f0.Radius | 2.0 | Sphere radius |
| Intensity | 1.0 | scaling factor |
| Radius | 2.0 | Sphere radius, in Angstroms |
| Diffusion | 0.05 | Diffusion coefficient, in units of A^2*THz, if energy in meV, or A^2*PHz if energy in ueV |
| Shift | 0.0 | Shift in domain |
Categories: FitFunctions | QuasiElastic