Table of Contents
Calculates attenuation due to absorption and scattering in a sample & its environment using a Monte Carlo.
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | The name of the input workspace. The input workspace must have X units of wavelength. |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | The name to use for the output workspace. |
| NumberOfWavelengthPoints | Input | number | Optional | The number of wavelength points for which a simulation is atttempted (default: all points) |
| EventsPerPoint | Input | number | 300 | The number of “neutron” events to generate per simulated point |
| SeedValue | Input | number | 123456789 | Seed the random number generator with this value |
This algorithm performs a Monte Carlo simulation to calculate the correction factors due to attenuation & single scattering within a sample plus optionally its sample environment.
The algorithm will compute the correction factors on a bin-by-bin basis for each spectrum within the input workspace. The following assumptions on the input workspace will are made:
By default the beam is assumed to be the a slit with width and height matching the width and height of the sample. This can be overridden using SetBeam.
By default, the material for the sample & containers will define the values of the cross section used to compute the absorption factor and will include contributions from both the total scattering cross section & absorption cross section. This follows the Hamilton-Darwin [1], [2] approach as described by T. M. Sabine in the International Tables of Crystallography Vol. C [3].
The algorithm proceeds as follows. For each spectrum:
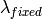 )
)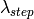 )
)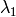 as the wavelength before scattering &
as the wavelength before scattering & 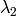 as wavelength after scattering:
as wavelength after scattering: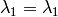 ,
, 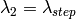
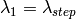 ,
, 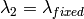
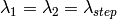
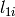
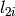
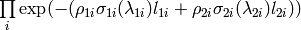 where
where 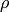 is the mass density of the material &
is the mass density of the material &
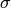 the absorption cross-section at a given wavelength
the absorption cross-section at a given wavelength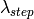 .
.Example: A cylindrical sample with no container
data = CreateSampleWorkspace(WorkspaceType='Histogram', NumBanks=1)
data = ConvertUnits(data, Target="Wavelength")
# Default up axis is Y
SetSample(data, Geometry={'Shape': 'Cylinder', 'Height': 5.0, 'Radius': 1.0,
'Center': [0.0,0.0,0.0]},
Material={'ChemicalFormula': '(Li7)2-C-H4-N-Cl6', 'SampleNumberDensity': 0.07})
# Simulating every data point can be slow. Use a smaller set and interpolate
abscor = MonteCarloAbsorption(data, NumberOfWavelengthPoints=50)
corrected = data/abscor
Example: A cylindrical sample setting a beam size
data = CreateSampleWorkspace(WorkspaceType='Histogram', NumBanks=1)
data = ConvertUnits(data, Target="Wavelength")
# Default up axis is Y
SetSample(data, Geometry={'Shape': 'Cylinder', 'Height': 5.0, 'Radius': 1.0,
'Center': [0.0,0.0,0.0]},
Material={'ChemicalFormula': '(Li7)2-C-H4-N-Cl6', 'SampleNumberDensity': 0.07})
SetBeam(data, Geometry={'Shape': 'Slit', 'Width': 0.8, 'Height': 1.0})
# Simulating every data point can be slow. Use a smaller set and interpolate
abscor = MonteCarloAbsorption(data, NumberOfWavelengthPoints=50)
corrected = data/abscor
Example: A cylindrical sample with predefined container
The following example uses a test sample environment defined for the TEST_LIVE facility and ISIS_Histogram instrument and assumes that these are set as the default facility and instrument respectively. The definition can be found at [INSTALLDIR]/instrument/sampleenvironments/TEST_LIVE/ISIS_Histogram/CRYO-01.xml.
data = CreateSampleWorkspace(WorkspaceType='Histogram', NumBanks=1)
data = ConvertUnits(data, Target="Wavelength")
# Sample geometry is defined by container but not completely filled so
# we just define the height
SetSample(data, Environment={'Name': 'CRYO-01', 'Container': '8mm'},
Geometry={'Height': 4.0},
Material={'ChemicalFormula': '(Li7)2-C-H4-N-Cl6', 'SampleNumberDensity': 0.07})
# Simulating every data point can be slow. Use a smaller set and interpolate
abscor = MonteCarloAbsorption(data, NumberOfWavelengthPoints=30)
corrected = data/abscor
| [1] | Darwin, C. G., Philos. Mag., 43 800 (1922) doi: 10.1080/10448639208218770 |
| [2] | Hamilton, W.C., Acta Cryst, 10, 629 (1957) doi: 10.1107/S0365110X57002212 |
| [3] | Sabine, T. M., International Tables for Crystallography, Vol. C, Page 609, Ed. Wilson, A. J. C and Prince, E. Kluwer Publishers (2004) doi: 10.1107/97809553602060000103 |
Categories: Algorithms | CorrectionFunctions\AbsorptionCorrections