InelasticDiffRotDiscreteCircle¶

Description¶

Summary¶

This fitting function models the inelastic part of the dynamics structure factor of a particle undergoing discrete jumps on N-sites evenly distributed in a circle. The particle can only jump to neighboring sites. This is the most common type of discrete rotational diffusion in a circle.

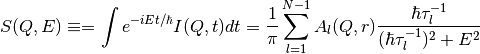
$S(Q,E) \equiv = \int e^{-iEt/\hbar} I(Q,t) dt = \frac{1}{\pi} \sum_{l=1}^{N-1} A_l (Q,r) \frac{\hbar \tau_l^{-1}}{(\hbar \tau_l^{-1})^2+E^2}$

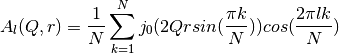
$A_l(Q,r) = \frac{1}{N} \sum_{k=1}^{N} j_0( 2 Q r sin(\frac{\pi k}{N}) ) cos(\frac{2\pi lk}{N})$

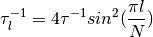
$\tau_l^{-1} = 4 \tau^{-1} sin^2(\frac{\pi l}{N})$

with h = 4.135665616 meV ps.

This function makes up the inelastic part of DiffRotDiscreteCircle.

Attributes (non-fitting parameters)¶

Name	Type	Default	Description
N
Q
WorkspaceIndex

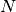$N$ (integer, default=3) number of sites - 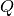$Q$ (double, default=0.5) Momentum transfer - 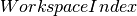$WorkspaceIndex$ (integer, default=0)

Properties (fitting parameters)¶

Name	Default	Description
Intensity	1.0	scaling factor [no units]
Radius	1.0	Circle radius [Angstroms]
Decay	1.0	Inverse of transition rate, in nanoseconds if energy in micro-ev, or picoseconds if energy in mili-eV
Shift	0.0	Shift in the centre of the peak

Categories: FitFunctions | QuasiElastic

Source¶

C++ source: InelasticDiffRotDiscreteCircle.cpp (last modified: 2019-06-04)

C++ header: InelasticDiffRotDiscreteCircle.h (last modified: 2018-10-05)