This fitting function models the inelastic part of the dynamics structure factor of a particle undergoing continuous diffusion but confined to a spherical volume, DiffSphere.
![S(Q,E\equiv \hbar \omega) = \frac{1}{\pi} \sum_{l=1}^{N-1} (2l+1) A_{n,l} (Q\cdot R) \frac{x_{n,l}^2 D/R^2}{[x_{n,l}^2 D/R^2]^21+\omega^2}](../../_images/math/d2d7f29113f809df0f6c42c3748f29a09a87ce91.png)
![A_{n,l} = \frac{6x_{n,l}^2}{x_{n,l}^2-l(l+1)} [\frac{QRj_{l+1}(QR) - lj_l(QR)}{(QR)^2 - x_{n,l}^2}]^2](../../_images/math/cb26e1496d6c83b62a8f27bb485bf90d2366691b.png)
Because of the spherical symmetry of the problem, the structure factor
is expressed in terms of the 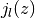 spherical Bessel functions.
spherical Bessel functions.
The value of the momentum transfer can be obtained either through
attribute 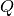 , or can be calculated from the input workspace
using attribute
, or can be calculated from the input workspace
using attribute 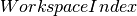 . The value calculated
using the workspace is used whenever attribute
. The value calculated
using the workspace is used whenever attribute 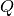 is set empty.
is set empty.
| Name | Type | Default | Description |
|---|---|---|---|
| Q | |||
| WorkspaceIndex |
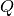 (double, default=1.0) Momentum transfer -
(double, default=1.0) Momentum transfer -
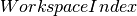 (integer, default=0)
(integer, default=0)
| Name | Default | Description |
|---|---|---|
| Intensity | 1.0 | scaling factor |
| Radius | 2.0 | Sphere radius, in Angstroms |
| Diffusion | 0.05 | Diffusion coefficient, in units of A^2*THz, if energy in meV, or A^2*PHz if energy in ueV |
| Shift | 0.0 | Shift in domain |
Categories: FitFunctions | QuasiElastic
C++ source: InelasticDiffSphere.cpp (last modified: 2019-07-17)
C++ header: InelasticDiffSphere.h (last modified: 2018-10-05)