\(\renewcommand\AA{\unicode{x212B}}\)
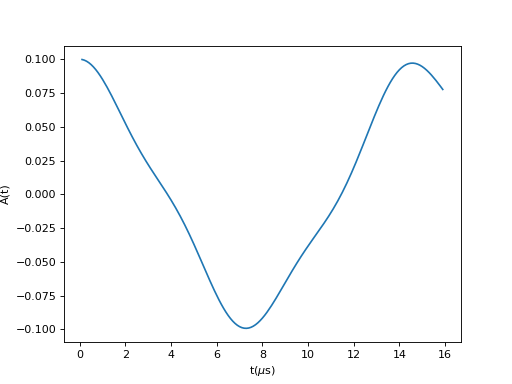
A relaxation function for a pair of transver field triplet muonium frequencies.
and,
where,
\(A_0\) is the amplitude,
A (MHz) is the isotropic hyperfine coupling constant,
\(\phi\) (rad) is the phase at time \(t=0\),
\(g_\mu = 0.01355342\) , the gyromagnetic ratio of muon,
\(g_e = 2.8024\) , the gyromagnetic ratio of electron,
and \(f_\text{cut} = 10^{32}\) (MHz).
(Source code, png, hires.png, pdf)
| Name | Default | Description |
|---|---|---|
| A0 | 0.2 | Amplitude |
| Field | 0.1 | Magnetic Field (G) |
| A | 0.2 | Isotropic hyperfine coupling constant (MHz) |
| Phi | 0.0 | Phase (rad) |
[1] P. Percival, TRIUMF Summer Institute 2011.
[2] F.L. Pratt, Physica B 289-290, 710 (2000).
Categories: FitFunctions | Muon\MuonSpecific
Python: LowTFMuonium.py (last modified: 2020-03-20)