6.1

\(\renewcommand\AA{\unicode{x212B}}\)

Meier

Description

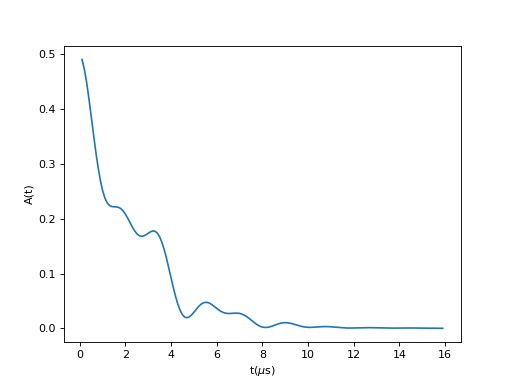
Time dependence of the polarization function for a static muon interacting with nuclear spin [1].

\[A(t)=\frac13(2P_x+P_z)\]

,where

\[P_z(t) = \frac{1}{2J+1}\left\{1+\sum^J_{m=-J+1}[\cos^2(2\alpha_m)+\sin^2(2\alpha_m)\cos(\lambda^+_m-\lambda^-_m)t]\right\},\]
\[P_x(t) = \frac{1}{2J+1}\sum^J_{m=-J} \{ \cos^2\alpha_{m+1}\sin^2\alpha_m\cos(\lambda_{m+1}^+-\lambda_m^+)t +\cos^2\alpha_{m+1}\cos^2\alpha_m\cos(\lambda_{m+1}^+-\lambda_m^-)t +\sin^2\alpha_{m+1}\sin^2\alpha_m\cos(\lambda_{m+1}^--\lambda_m^+)t +\sin^2\alpha_{m+1}\cos^2\alpha_m\cos(\lambda_{m+1}^--\lambda_m^-)t\},\]
\[\lambda_m^\pm = \frac{1}{2}[\omega_Q(2m^2-2m+1)+\omega_D\pm W_m],\]
\[W_m = \{(\omega_D+\omega_Q)^2(2m-1)^2+\omega_D^2[J(J+1)-m(m-1)]\}^\frac{1}{2},\]
\[\tan(2\alpha_m)=\frac{\omega_D[J(J+1)-m(m-1)]^\frac{1}{2}}{(1-2m)(\omega_D+\omega_Q)},\]

\(\omega_D\) is the angular frequency due to dipolar coupling,

\(\omega_Q\) is the angular frequency due to quadrupole interaction of the nuclear spin \(J\) due to a field gradient exerted by the presence of the muon,

\(J\) is the total angular momentum quantum number,

and \(m\) is the z-component of the total orbital quantum number.

(Source code, png, hires.png, pdf)

../../_images/Meier-1.png

Properties (fitting parameters)

Name Default Description
A0 0.5 Amplitude
FreqD 0.01 Frequency due to dipolar coupling (MHz)
FreqQ 0.05 Frequency due to quadrupole interaction of the nuclear spin (MHz)
Spin 3.5 J, Total angular momentum quanutm number
Sigma 0.2 Gaussian decay rate
Lambda 0.1 Exponential decay rate

Categories: FitFunctions | Muon\MuonSpecific

Source

Python: Meier.py (last modified: 2020-03-20)