\(\renewcommand\AA{\unicode{x212B}}\)
Table of Contents
| Name | Direction | Type | Default | Description |
|---|---|---|---|---|
| InputWorkspace | Input | MatrixWorkspace | Mandatory | Measured POLDI 2D-spectrum. |
| PoldiPeakWorkspace | Input | Workspace | Mandatory | Table workspace with peak information. |
| PeakProfileFunction | Input | string | Gaussian | Profile function to use for integrating the peak profiles before calculating the spectrum. Allowed values: [‘BackToBackExponential’, ‘Bk2BkExpConvPV’, ‘DeltaFunction’, ‘ElasticDiffRotDiscreteCircle’, ‘ElasticDiffSphere’, ‘ElasticIsoRotDiff’, ‘ExamplePeakFunction’, ‘Gaussian’, ‘IkedaCarpenterPV’, ‘Lorentzian’, ‘PseudoVoigt’, ‘Voigt’] |
| GlobalParameters | Input | string | Comma-separated list of parameter names that are identical for all peaks, is ignored when PawleyFit is selected. | |
| PawleyFit | Input | boolean | False | Instead of refining individual peaks, refine a unit cell. Peaks must be indexed using PoldiIndexKnownCompounds. |
| FitConstantBackground | Input | boolean | True | Add a constant background term to the fit. |
| ConstantBackgroundParameter | Input | number | 0 | Initial value of constant background. |
| FitLinearBackground | Input | boolean | True | Add a background term linear in 2theta to the fit. |
| LinearBackgroundParameter | Input | number | 0 | Initial value of linear background. |
| MaximumIterations | Input | number | 0 | Maximum number of iterations for the fit. Use 0 to calculate 2D-spectrum without fitting. |
| OutputWorkspace | Output | MatrixWorkspace | Mandatory | Calculated POLDI 2D-spectrum |
| Calculated1DSpectrum | Output | MatrixWorkspace | Mandatory | Calculated POLDI 1D-spectrum. |
| LambdaMin | Input | number | 1.1 | Minimum wavelength for 1D spectrum calculation |
| LambdaMax | Input | number | 5 | Maximum wavelength for 1D spectrum calculation |
| RefinedPoldiPeakWorkspace | Output | Workspace | Mandatory | Table workspace with fitted peaks. |
| OutputIntegratedIntensities | Input | boolean | False | If this option is checked, the peaks in the algorithm’s output will have integrated intensities instead of the maximum. |
| RefinedCellParameters | Output | Workspace | ||
| RawFitParameters | Output | Workspace | Table workspace that contains all raw fit parameters. |
PoldiFitPeaks2D is an algorithm that can be used to fit a set of individual peaks to 2D POLDI-data. These must come in a table of special format, which may be generated for example by PoldiFitPeaks1D v2. Furthermore, the algorithm needs a MatrixWorkspace containing raw POLDI data with correct dimensions and a proper instrument definition.
The 1D-peak intensities need to be integral intensities, so the peaks are integrated if necessary. If there is no profile information supplied in the peak table (PoldiFitPeaks1D v2 adds this automatically), it’s possible to supply a profile function as parameter to this algorithm. If a profile function name is present in the peak table, the one supplied in the parameters has priority.
There are two modes for performing the fit. In the default mode, all peak profiles are fitted independently using the same function that is used for integration. For profile functions other than Gaussian or Lorentzian it can be necessary to tie the additional profile parameters (for example the “Mixing” parameter of PseudoVoigt) so that they are the same for all peaks in order to get a reasonable fit. This can be achieved by specifying the names of these parameters in a comma separated list to the “GlobalParameters” property.
The other possibility is to perform a Pawley-type fit, where peak positions are calculated using lattice parameters and Miller indices (see PawleyFit v1 for a more general explanation of the method). This mode is controlled by the PawleyFit parameter. For these fits, an additional table will be created which contains the refined lattice parameters. Please note that the peaks need to be indexed to use this mode (using PoldiCreatePeaksFromCell v1 and PoldiIndexKnownCompounds v1).
Alternatively, if the peaks have been indexed using a different method, the log values UnitCell and CrystalSystem must be set on the table workspace using AddSampleLog v1. UnitCell must contain a string with 6 numbers that define a unit cell, with lengths in \(\mathrm{\AA{}}\) and angles in degree (for example 5.4 5.4 5.4 90 90 90), whereas CrystalSystem must be one of the seven crystal systems (for example Cubic).
PoldiFitPeaks2D can also be used to calculate a theoretical 2D pattern from a set of peaks by limiting the iterations to 0.
In addition to performing the 2D-fit, a theoretical 1D-diffractogram of the fit-function is calculated as well, which can be used in conjunction with PoldiAnalyseResiduals v1 to assess the quality of a fit. Depending on the value of the OutputIntegratedIntensity-option, the output peaks intensities are either integrated or describe the maximum.
Note
To run these usage examples please first download the usage data, and add these to your path. In Mantid this is done using Manage User Directories.
Individual peak profiles
PoldiFitPeaks2D operates on a MatrixWorkspace with a valid POLDI instrument definition. The following short example demonstrates how to use the algorithm, processing data obtained from recording the spectrum of a Silicon standard material (powder) and calculating a theoretical 2D-spectrum.
# Load data file with Si spectrum and instrument definition
truncated = PoldiLoadRuns(2013, 6904)
# Perform correlation, peak search and fit
correlated_6904 = PoldiAutoCorrelation("truncated_data_6904")
peaks_6904 = PoldiPeakSearch(correlated_6904)
PoldiFitPeaks1D(InputWorkspace = correlated_6904, FwhmMultiples = 4.0,
PeakFunction = "Gaussian", PoldiPeakTable = peaks_6904,
OutputWorkspace = "peaks_refined_6904",
FitPlotsWorkspace = "fit_plots_6904")
# Calculate a 2D spectrum using the refined peaks
PoldiFitPeaks2D(InputWorkspace="truncated_data_6904",
PoldiPeakWorkspace="peaks_refined_6904",
RefinedPoldiPeakWorkspace="peaks_fit_2d_6904",
Calculated1DSpectrum="simulated_1d_6904",
OutputWorkspace="simulated_6904")
After this step, there is a new workspace containing the simulated spectrum. It should look similar to the one in the following figure:
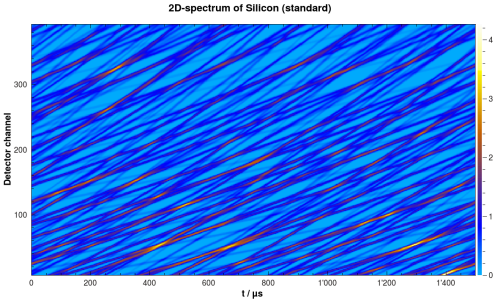
Simulated 2D-spectrum of silicon powder.
In general, there is a background in POLDI data that depends on \(2\theta\). The following script, which is almost identical to the above one introduces this parameter.
# Load data file with Si spectrum and instrument definition
truncated = PoldiLoadRuns(2013, 6904)
# Perform correlation, peak search and fit
correlated_6904 = PoldiAutoCorrelation("truncated_data_6904")
peaks_6904 = PoldiPeakSearch(correlated_6904)
PoldiFitPeaks1D(InputWorkspace = correlated_6904, FwhmMultiples = 4.0,
PeakFunction = "Gaussian", PoldiPeakTable = peaks_6904,
OutputWorkspace = "peaks_refined_6904",
FitPlotsWorkspace = "fit_plots_6904")
# Calculate a 2D spectrum using the refined peaks - with background linear in 2theta
PoldiFitPeaks2D(InputWorkspace="truncated_data_6904",
PoldiPeakWorkspace="peaks_refined_6904",
OutputWorkspace="simulated_6904",
RefinedPoldiPeakWorkspace="peaks_fit_2d_6904",
Calculated1DSpectrum="simulated_1d_6904",
LinearBackgroundParameter=0.01)
Now the spectrum looks different, like in the example below.
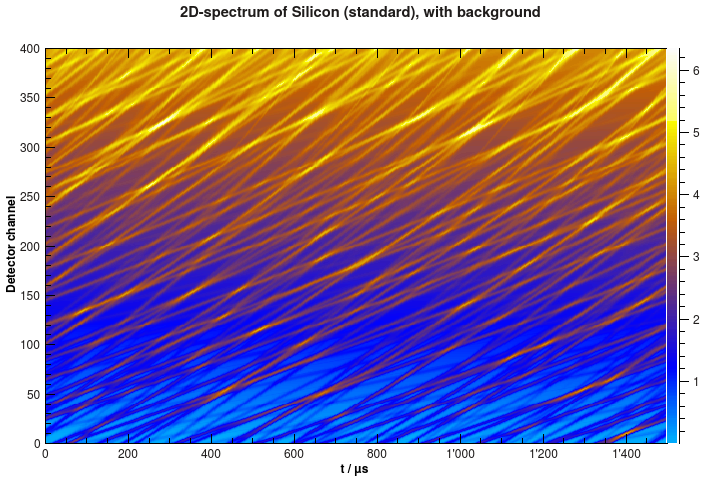
Simulated 2D-spectrum of silicon powder with background.
Furthermore, a 1D diffractogram is also calculated, which shows all peaks that were used to calculate the 2D spectrum as well.
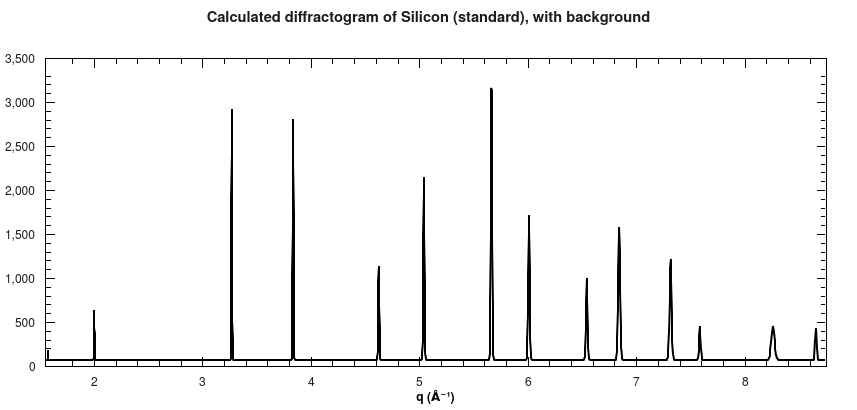
Calculated diffractogram for Silicon powder standard.
Pawley-type fit
The following example shows an example for refinement of lattice parameters using the PawleyFit-option.
import numpy as np
# Load and merge 2 data files for better statistics.
truncated = PoldiLoadRuns(2013, 6903, 6904, 2)
# Perform correlation, peak search and fit
correlated_6904 = PoldiAutoCorrelation("truncated_data_6904")
peaks_6904 = PoldiPeakSearch(correlated_6904)
PoldiFitPeaks1D(InputWorkspace = correlated_6904, FwhmMultiples = 4.0,
PeakFunction = "Gaussian", PoldiPeakTable = peaks_6904,
OutputWorkspace = "peaks_refined_6904",
FitPlotsWorkspace = "fit_plots_6904")
# Generate reflections for Silicon
si_peaks = PoldiCreatePeaksFromCell(SpaceGroup = "F d -3 m",
Atoms = "Si 0.0 0.0 0.0",
a = 5.431,
LatticeSpacingMin = 0.7)
# Index the refined peaks
indexed = PoldiIndexKnownCompounds("peaks_refined_6904",
CompoundWorkspaces = "si_peaks")
# Only consider the first 8 peaks
DeleteTableRows("peaks_refined_6904_indexed_si_peaks", "8-30")
# Fit a unit cell.
PoldiFitPeaks2D(InputWorkspace="truncated_data_6904",
PoldiPeakWorkspace="peaks_refined_6904_indexed_si_peaks",
OutputWorkspace="fitted_6904",
PawleyFit = True,
MaximumIterations=100,
RefinedPoldiPeakWorkspace="peaks_fit_2d_6904",
Calculated1DSpectrum="simulated_1d_6904",
RefinedCellParameters="refined_cell_6904")
lattice_parameters = AnalysisDataService.retrieve("refined_cell_6904")
cell_a = np.round(lattice_parameters.cell(0, 1), 5)
cell_a_error = np.round(lattice_parameters.cell(0, 2), 5)
print("Refined lattice parameter a = {:.5f} +/- {}".format(cell_a, cell_a_error))
The refined lattice parameter is printed at the end:
Refined lattice parameter a = 5.43126 +/- 4e-05
Categories: AlgorithmIndex | SINQ\Poldi