\(\renewcommand\AA{\unicode{x212B}}\)

IntegrateEllipsoids v1¶

Summary ¶

Integrate Single Crystal Diffraction Bragg peaks using 3D ellipsoids.

Properties ¶

Name	Direction	Type	Default	Description
InputWorkspace	Input	MatrixWorkspace	Mandatory	An input MatrixWorkspace with time-of-flight units along X-axis and defined instrument with defined sample
PeaksWorkspace	InOut	PeaksWorkspace	Mandatory	Workspace with Peaks to be integrated. NOTE: The peaks MUST be indexed with integer HKL values.
RegionRadius	Input	number	0.35	Only events at most this distance from a peak will be considered when integrating
SpecifySize	Input	boolean	False	If true, use the following for the major axis sizes, else use 3-sigma
PeakSize	Input	number	0.18	Half-length of major axis for peak ellipsoid
BackgroundInnerSize	Input	number	0.18	Half-length of major axis for inner ellipsoidal surface of background region
BackgroundOuterSize	Input	number	0.23	Half-length of major axis for outer ellipsoidal surface of background region
OutputWorkspace	Output	PeaksWorkspace	Mandatory	The output PeaksWorkspace will be a copy of the input PeaksWorkspace with the peaks’ integrated intensities.
CutoffIsigI	Input	number	Optional	Cuttoff for I/sig(i) when finding mean of half-length of major radius in first pass when SpecifySize is false.Default is no second pass.
NumSigmas	Input	number	3	Number of sigmas to add to mean of half-length of major radius for second pass when SpecifySize is false.
IntegrateInHKL	Input	boolean	False	If true, integrate in HKL space not Q space.
IntegrateIfOnEdge	Input	boolean	True	Set to false to not integrate if peak radius is off edge of detector.Background will be scaled if background radius is off edge.
AdaptiveQBackground	Input	boolean	False	Default is false. If true, BackgroundOuterRadius + AdaptiveQMultiplier * \|Q\| and BackgroundInnerRadius + AdaptiveQMultiplier * \|Q\|
AdaptiveQMultiplier	Input	number	0	PeakRadius + AdaptiveQMultiplier * \|Q\| so each peak has a different integration radius. Q includes the 2*pi factor.
UseOnePercentBackgroundCorrection	Input	boolean	True	If this options is enabled, then the top 1% of the background will be removedbefore the background subtraction.
SatelliteRegionRadius	Input	number	0.1	Only events at most this distance from a peak will be considered when integrating
SatellitePeakSize	Input	number	0.08	Half-length of major axis for satellite peak ellipsoid
SatelliteBackgroundInnerSize	Input	number	0.08	Half-length of major axis for inner ellipsoidal surface of satellite background region
SatelliteBackgroundOuterSize	Input	number	0.09	Half-length of major axis for outer ellipsoidal surface of satellite background region
GetUBFromPeaksWorkspace	Input	boolean	False	If true, UB is taken from peak workspace.

This algorithm will integrate disjoint single crystal Bragg peaks and satellites (See ModulatedStructure) by summing the number of raw or weighted events in a 3D ellipsoidal peak region in reciprocal space (See IntegrateInHKL option for integrating in HKL) and subtracting an estimate of the background obtained from an ellipsoidal shell. In some ways it is similar to the IntegratePeaksMD v2 algorithm. In particular the size parameters to this algorithm are also specified in inverse Angstroms and the background subtraction is done in the same way for both the intensity and the estimated standard deviations. However, this algorithm differs from IntegratePeaksMD v2 in several critical ways.

This algorithm works directly with raw or weighted events while IntegratePeaksMD v2 uses MDEvents from MDEventWorkspace.
This algorithm uses 3D ellipsoidal regions with aspect ratios that are adapted to the set of events that are near the peak center, while IntegratePeaksMD v2 uses spherical regions.
This algorithm includes an option to automatically choose the size of the ellipsoidal regions based on the statistics of the set of events near the peak.
This algorithm only applies to peaks with integral HKL values and as currently implemented it cannot be used to integrate ellipsoidal regions at other locations in reciprocal space.

The algorithm calculates the three principal axes of the events near a peak, and uses the standard deviations in the directions of the principal axes to determine the aspect ratio of ellipsoids used for the peak and background regions.

Explanation of Inputs ¶

The event data to be integrated is obtained from an ordinary EventWorkspace with an X-axis in time-of-flight, as loaded from a NeXus event file. This algorithm maps the events to reciprocal space using PeaksWorkwpace with indexed peaks to determine the parameters of the transformation into the reciprocal space (UB matrix)
The peaks to be integrated are are also obtained from a PeaksWorkspace. The peaks must be indexed, and any peaks indexed as (0,0,0) will be ignored. The HKL values for valid peaks should all be integers, to make this check for unindexed peaks reliable.
Only events that are near a peak are considered when constructing the ellipsoids. The RegionRadius specifies the maximum distance from the peak center to an event in reciprocal space, for that event to used. See the figure below. Also, each event will be counted for at most one peak, the one with the nearest HKL value. The RegionRadius should be specified to be just slightly larger than the expected peak region to avoid overlap with other peaks, and to avoid including excessive background. As the size of the RegionRadius increases, the ellipsoids will become more spherical and less well adapted to the actual shape of the peak.

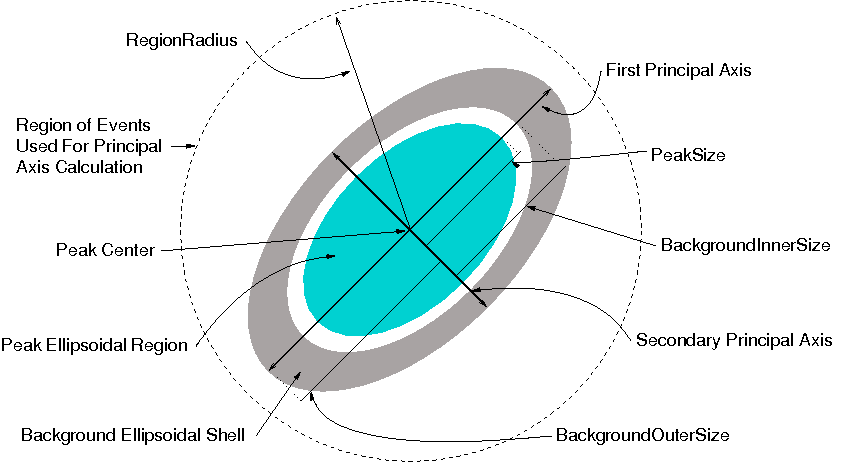
Integrate ellipsoids algorithm regions map.¶

If the SpecifySize option is selected, then the user MUST specify the PeakSize, BackgroundInnerSize and BackgroundOuterSize. In this mode, the algorithm is similar to the IntegratePeaksMD v2 algorithm. As shown in the figure, these values determine the length of the major axis for the ellipsoidal peak region, and of the inner and outer ellipsoids bounding the background region. The same major axis lengths are used for all peaks, but the lengths of the other two axes of the ellipsoids are adjusted based on the standard deviations of the events in those directions. If SpecifySize is false, then the major axis length for each peak will be set to include a range of plus or minus three times the standard deviation of the events in that direction. That is, PeakSize is set to three times the standard deviation in the direction of the first principal axis. Also, in this case the BackgroundInnerSize is set to the PeakSize and the BackgroundOuterSize is set so that the background ellipsoidal shell has the same volume as the peak ellipsoidal region. If specified by the user, these parameters must be ordered correctly with: \(0 < PeakSize \leq BackgroundInnerSize\) and \(BackgroundInnerSize < BackgroundOuterSize \leq RegionRadius\)
If UseOnePercentBackgroundCorrection is enabled, then the top 1% of the background events are removed so that there are no intensity spikes near the edges. This is enabled by default.
AdaptiveQMultiplier can be used with SpecifySize for the radius to vary as a function of the modulus of Q. If the AdaptiveQBackground option is set to True, the background radius also changes so each peak has a different integration radius. Q includes the 2*pi factor.
- PeakRadius + AdaptiveQMultiplier * |Q|
- BackgroundOuterRadius + AdaptiveQMultiplier * |Q|
- BackgroundInnerRadius + AdaptiveQMultiplier * |Q|
If the IntegrateInHKL option is selected, then HKL space is used for the integration instead of reciprocal space. This option may be useful for large unit cells where the radius of integration needs to be very different for peaks at low Q and high Q. With this option the PeakSize, BackgroundInnerSize and BackgroundOuterSize are specified in HKL and they just need to be smaller than 0.5.
The integrated intensities will be set in the specified OutputWorkspace. If this is different from the input PeaksWorkspace, the input peaks workspace will be copied to the OutputWorkspace before setting the integrated intensities.

Detailed Algorithm Description ¶

This algorithm will integrate a list of indexed single-crystal diffraction peaks from a PeaksWorkspace, using events from an ( EventWorkspace ). The indexed peaks are first used to determine a UB matrix. The inverse of that UB matrix is then used to form lists of events that are close to peaks in reciprocal space. An event will be added to the list of events for a peak provided that the fractional \(h,k,l\) value of that event (obtained by applying UB-inverse to the \(Q\) -vector) is closer to the \(h,k,l\) of that peak, than to the \(h,k,l\) of any other peak AND the \(Q\) -vector for that event is within the specified radius of the \(Q\) -vector for that peak. This technique makes the algorithm suitable for nuclear peaks, but may not be suitable for magnetic peaks.

When the lists of events near the peaks have been built, the three principal axes of the set of events near each peak are found, and the standard deviations of the projections of the events on each of the three principal axes are calculated. The principal axes and standard deviations for the events around a peak in the directions of the principal axes are used to determine an ellipsoidal region for the peak and an ellipsoidal shell region for the background. The number of events in the peak ellipsoid and background ellipsoidal shell are counted and used to determine the net integrated intensity of the peak.

The ellipsoidal regions used for the peak and background can be obtained in two ways. First, the user may specify the size of the peak ellipsoid and the inner and outer size of the background ellipsoid. If these are specified, the values will be used for half the length of the major axis of an ellipsoid centered on the peak. The major axis is in the direction of the principal axis for which the standard deviation in that direction is largest. The other two axes for the ellipsoid are in the direction of the other two principal axes and are scaled relative to the major axes in proportion to their standard deviations. For example if the standard deviations in the direction of the other two principal axes are .8 and .7 times the standard deviation in the direction of the major axis, then the ellipse will extend only .8 and .7 times as far in the direction of those axes, as in the direction of the major axis. Overall, the user specified sizes for the PeakSize, BackgroundInnerSize and BackgroundOuterSize are similar to the PeakRadius, BackgroundInnerRadius and BackgrounOuterRadius for the IntegratePeaksMD v2 algorithm. The difference is that the regions used in this algorithm are not spherical, but are ellipsoidal with axis directions obtained from the principal axes of the events near a peak and the ellipsoid shape (relative axis lengths) is determined by the standard deviations in the directions of the principal axes.

Second, if the user does not specify the size of the peak and background ellipsoids, then the three axes of the peak ellipsoid are again set to the principal axes of the set of nearby events but in this case their axis lengths are set to cover a range of plus or minus three standard deviations in the axis directions. In this case, the background ellipsoidal shell is chosen to have the same volume as the peak ellipsoid and it’s inner surface is the outer surface of the peak ellipsoid. The outer surface of the background ellipsoidal shell is an ellipsoidal surface with the same relative axis lengths as the inner surface.

This algorithm uses principle component analysis to determine the principle axis for each peak. For the event list (QLab) associated with each peak, the algorithm determines a covariance matrix, and uses that to establish eigenvectors corresponding to the principle axis (all orthogonal). The sizes of each principle axis are used define the region of which events will be counted/integrated from those already associated with each peak.

IntegrateIfOnEdge=False option ¶

Edges for each bank or pack of tubes of the instrument are defined by masking the edges in the PeaksWorkspace instrument. e.g. For CORELLI, tubes 1 and 16, and pixels 0 and 255. Q in the lab frame for every peak is calculated, call it C For every point on the edge, the trajectory in reciprocal space is a straight line, going through:

\(\vec{O}=(0,0,0)\)

Calculate a point at a fixed momentum, say k=1. Q in the lab frame:

\(\vec{E}=(-k*sin(\theta)*cos(\phi),-k*sin(\theta)*sin(\phi),k-k*cos(\phi))\)

Normalize E to 1:

\(\vec{E}=\vec{E}*(1./\left|\vec{E}\right|)\)

The distance from C to OE is given by:

\(dv=\vec{C}-\vec{E}*(\vec{C} \cdot \vec{E})\)

If:

\(\left|dv\right|<PeakRadius\)

for the integration, one of the detector trajectories on the edge is too close to the peak This method is also applied to all masked pixels. If there are masked pixels trajectories inside an integration volume, the peak must be rejected. If there are masked pixel trajectories inside the background volume, the background events are scaled by estimating the volume of the ellipsoid on the detector.

Sigma from the background ¶

The sigma from the background could be too small because the background contains events from other peaks. In an effort to reduce this, all the background events are sorted and the top 1% are removed. Note that this behaviour is optional and can be enabled if the property UseOnePercentBackgroundCorrection is enabled. It is enabled by default.

Usage ¶

Example - IntegrateEllipsoids:

User should provide their own event nexus file instead of TOPAZ_3132_event.nxs used within this example. The original TOPAZ_3132_event.nxs file is available in Mantid system tests repository.

def print_tableWS(pTWS,nRows):
    ''' Method to print part of the table workspace '''
    tab_names=pTWS.keys()
    row = ""
    for name in tab_names:
        if len(name)>8:
           name= name[:8]
        row += "| {:8} ".format(name)
    print(row + "|")

    for i in range(nRows):
        row = ""
        for name in tab_names:
              col = pTWS.column(name);
              data2pr=col[i]
              if type(data2pr) is float:
                  row += "| {:8.1f} ".format(data2pr)
              else:
                  row += "| {:8} ".format(str(data2pr))
        print(row + "|")

# load test workspace
Load(Filename=r'TOPAZ_3132_event.nxs',OutputWorkspace='TOPAZ_3132_event',LoadMonitors='1')

# build peak workspace necessary for IntegrateEllipsoids algorithm to work
ConvertToMD(InputWorkspace='TOPAZ_3132_event',QDimensions='Q3D',dEAnalysisMode='Elastic',Q3DFrames='Q_sample',LorentzCorrection='1',OutputWorkspace='TOPAZ_3132_md',\
MinValues='-25,-25,-25',MaxValues='25,25,25',SplitInto='2',SplitThreshold='50',MaxRecursionDepth='13',MinRecursionDepth='7')
FindPeaksMD(InputWorkspace='TOPAZ_3132_md',PeakDistanceThreshold='0.3768',MaxPeaks='50',DensityThresholdFactor='100',OutputWorkspace='TOPAZ_3132_peaks')
FindUBUsingFFT(PeaksWorkspace='TOPAZ_3132_peaks',MinD='3',MaxD='15',Tolerance='0.12')
IndexPeaks(PeaksWorkspace='TOPAZ_3132_peaks',Tolerance='0.12')

# integrate Ellipsoids
result=IntegrateEllipsoids(InputWorkspace='TOPAZ_3132_event',PeaksWorkspace='TOPAZ_3132_peaks',\
       RegionRadius='0.25',PeakSize='0.2',BackgroundInnerSize='0.2',BackgroundOuterSize='0.25',OutputWorkspace='TOPAZ_3132_peaks')

# print 10 rows of resulting table workspace
print_tableWS(result,10)

Output:

| RunNumbe | DetID    | h        | k        | l        | Waveleng | Energy   | TOF      | DSpacing | Intens   | SigInt   | BinCount | BankName | Row      | Col      | QLab     | QSample  | PeakNumb |
| 3132     | 1124984  |     -2.0 |     -1.0 |      2.0 |      3.1 |      8.5 |  14482.3 |      2.0 | 120486.0 |    375.8 |   1668.0 | bank17   |    120.0 |     42.0 | [1.57771,1.21779,2.37854] | [2.99396,0.815958,0.00317344] | 1        |
| 3132     | 1156753  |     -3.0 |     -2.0 |      3.0 |      2.1 |     18.8 |   9725.7 |      1.3 | 149543.0 |    393.0 |   1060.0 | bank17   |    145.0 |    166.0 | [2.48964,1.45725,3.88666] | [4.52618,1.71025,0.129461] | 2        |
| 3132     | 1141777  |     -4.0 |     -2.0 |      3.0 |      1.7 |     28.1 |   7963.2 |      1.0 |   8744.0 |    106.3 |     96.0 | bank17   |     17.0 |    108.0 | [2.60836,2.31423,4.86391] | [5.69122,1.79492,-0.452799] | 3        |
| 3132     | 1125241  |     -4.0 |     -2.0 |      4.0 |      1.6 |     33.9 |   7252.2 |      1.0 |  19740.0 |    146.2 |     83.0 | bank17   |    121.0 |     43.0 | [3.15504,2.42573,4.75121] | [5.97829,1.63473,0.0118744] | 4        |
| 3132     | 1170598  |     -4.0 |     -3.0 |      4.0 |      1.5 |     34.1 |   7224.6 |      0.9 |  15914.0 |    131.4 |     73.0 | bank17   |    166.0 |    220.0 | [3.43363,1.70178,5.39301] | [6.07726,2.59962,0.281759] | 5        |
| 3132     | 1214951  |     -2.0 |     -1.0 |      4.0 |      1.9 |     22.8 |   8839.5 |      1.7 | 121852.0 |    352.9 |    719.0 | bank18   |    231.0 |    137.0 | [2.73683,1.43808,2.11574] | [3.5786,0.470838,1.00329] | 6        |
| 3132     | 1207827  |     -3.0 |     -1.0 |      4.0 |      1.7 |     27.9 |   7991.7 |      1.3 |  64593.0 |    257.7 |    447.0 | bank18   |     19.0 |    110.0 | [2.80324,2.29519,3.09134] | [4.71517,0.554412,0.37714] | 7        |
| 3132     | 1232949  |     -4.0 |     -2.0 |      6.0 |      1.2 |     53.3 |   5782.1 |      0.9 |  18247.0 |    139.3 |     45.0 | bank18   |     53.0 |    208.0 | [4.29033,2.63319,4.46168] | [6.52658,1.27985,1.00646] | 8        |
| 3132     | 1189484  |     -4.0 |     -1.0 |      6.0 |      1.1 |     63.4 |   5299.3 |      1.0 |  13512.0 |    120.7 |     31.0 | bank18   |    108.0 |     38.0 | [4.02414,3.39659,3.83664] | [6.4679,0.298896,0.726133] | 9        |
| 3132     | 1218337  |     -5.0 |     -2.0 |      7.0 |      1.0 |     79.8 |   4724.1 |      0.8 |   7411.0 |     88.3 |     15.0 | bank18   |     33.0 |    151.0 | [4.96622,3.61607,5.32554] | [7.99244,1.19363,0.892655] | 10       |